Overte, či je vektor platný pre maticu.

adsby.ru

SYSTÉM HOMOGÉNNYCH LINEÁRNYCH RIEK

Systém homogénnych lineárnych úrovní sa nazýva systém vo forme Je jasné, čo je na tom zlé

, pretože všetky prvky jedného z týchto zdrojov v týchto derivátoch sa stanú nulovými. Neviditeľné fragmenty hľadajú vzorce = , potom ak Δ ≠ 0, systém má len nulové riešenie = X r

z= 0. Prote, v mnohých závodoch nie je napájanie, a rovnaký systém je riešený ako nulový.

Veta.

Na to, aby sústava lineárnych homogénnych rovníc mala malé nenulové riešenia, je potrebné a postačujúce, aby Δ ≠ 0.

Preto, ak je premenná ≠ 0, potom je systém úplne nevyriešený.

Ak Δ ≠ 0, potom systém lineárnych homogénnych hladín je indiferentným riešením. , aplikujte to. VLASNY VEKTORY A VLASNAYA HODNOTOVÁ MATICE Dajme štvorcovú maticu. .

X aplikujte to.

- Matica je stohovaná, ktorej výška je v súlade s poradím matrice

A V bohatých pokladoch môžete vidieť bohatstvo de λ – deyake číslo. Dajme štvorcovú maticu Je jasné, že v každom prípade môže žiarlivosť viesť k nulovému rozlíšeniu. aplikujte to. Volá sa číslo λ, pre ktoré systém robí nenulové rozhodnutia Vlasnym významy de λ – deyake číslo. Dajme štvorcovú maticu.

matice Dajme štvorcovú maticu, A lebo také λ sa nazýva∙so silným vektorom Poznáme mocninový vektor matice . Oskolki .

E

X = X , potom je možné maticovú rovnicu prepísať do tvaru, alebo iný, . Otvorenejším spôsobom možno hodnosti prepísať ako systém lineárnych hodností. aplikujte to. Hodnotný

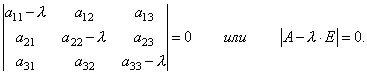
Ja potom, Teraz sme vytvorili systém homogénnych lineárnych súradníc de λ – deyake číslo. Dajme štvorcovú maticu x 1

x 2 aplikujte to. x 3

Na to, aby sústava lineárnych homogénnych rovníc mala malé nenulové riešenia, je potrebné a postačujúce, aby Δ ≠ 0.

vektor

.

Dovoľte nám predstaviť suvore vyznachennya.

Narovnané rezom takzvaný výrez, až na konci každého je jasné, ktorý je prvý a ktorý druhý.

Vektor Nazýva sa to priamy strih, je to teda pieseň dowzhin. Dajme štvorcovú maticu Toto je časť spievajúcej holubice, v ktorej jeden z bodov, ktorý oddeľuje jeden, je zachytený klasom a druhý - koncom. Yakshcho- vektorový klas,

B. – Nakoniec je vektor označený symbolom a okrem toho je vektor často označený jedným písmenom . Na dieťati je vektor označený sekciou ako priama šípka.

modul

dovzhina Vektor sa nazýva dovezhna počiatočného priameho rezu. znamenať |

chi ||. Pred vektormi ich nazývame nulový vektor, ktorého začiatok a koniec sú rovnaké..

Označuje sa Vin. Nulový vektor nemá priamu priamku a jeho modul sa rovná nule ||=0. Volám sa vektory i

Kolineárne

keďže smrad sa šíri na jednej priamke alebo na rovnobežných priamkach..

V tomto prípade sú však vektory narovnané, napísané a predĺžené.

1. Nazývajú sa vektory nakreslené na priamych čiarach rovnobežných s tou istou rovinou

   koplanárny

   Volajú sa dva vektory i

   

   rovný Hoci sú kolineárne, sú však narovnané a navzájom si rovné.

   Škoda písať. Kvôli dôležitosti vektorov to znamená, že vektor sa môže pohybovať rovnobežne so sebou samým a umiestniť jeho klas ako bod v priestore.:

2. Napríklad

   LINEÁRNE OPERÁCIE NA VEKTOROCH Násobenie vektora číslom. Pridanie k vektoru pre číslo λ je nový vektor taký, že: Dajme štvorcovú maticu Označuje sa pridanie vektora k číslu λ. Napríklad, je vektor, ktorý rektifikuje rovnakú stranu ako vektor a má dvojitý, dvojitý spodný vektor. .

   

   Prevádzka zavedená v máji orgány Skladacie vektory. Násobenie vektora číslom. Pustite a – ďalšie dva vektory. Zoberme si dostatočný bod O Násobenie vektora číslom. A my budeme vektor.

   

   Od veci Pridajme vektor..

3. Vektor, ktorý spája hlavu prvého vektora s koncom druhého, sa nazýva

   s taškou tieto vektory a sú označené vektor pre vektor i je označený .

Opačný vektor môže byť výsledkom vynásobenia vektora číslom λ = –1: . Prvá časť obsahuje ustanovenia, ktoré sú minimálne potrebné na pochopenie chemometrie, a druhá časť obsahuje fakty, ktoré je potrebné poznať pre hlbšie pochopenie metód analýzy bohatého sveta. Pracovný hárok je ilustrovaný zadkami, ktoré sa zobrazujú v excelovom zošite Matrix.xls

, ktorý je priložený k tomuto dokumentu.

Poznámky k aplikáciám sú umiestnené v texte ako objekt programu Excel. Tieto aplikácie sú abstraktného charakteru, nie sú viazané na špecifikácie analytickej chémie. Reálne aplikácie vikoristickej maticovej algebry v chemometrii sú diskutované v iných textoch venovaných rôznym chemometrickým prídavkom. Neviditeľné fragmenty hľadajú vzorce Väčšina experimentov, ktoré sa vykonávajú v analytickej chémii, nie sú priame, ale Neviditeľné fragmenty hľadajú vzorce nepriamy Neviditeľné fragmenty hľadajú vzorce. To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota(Signál), teda remíza, ale nerovná sa C. Neviditeľné fragmenty hľadajú vzorce(To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota(C) ≠ C. Spravidla typ skladovania (C) neznáme, našťastie, v analytickej chémii je väčšina svetov proporcionálna. To znamená, že pri vyšších koncentráciách C Neviditeľné fragmenty hľadajú vzorce a Neviditeľné fragmenty hľadajú vzorce krát sa signál X štýlovo zvýši. Neviditeľné fragmenty hľadajú vzorce C) = a x(C). Okrem toho sú signály viac aditívne, takže signál zo vzorky, v ktorej sú prítomné dve reči s koncentráciami C1 a C2, sa rovná súčtu signálov z kožnej zložky.(Ci + C2) = Neviditeľné fragmenty hľadajú vzorce 1 , Neviditeľné fragmenty hľadajú vzorce 2 ,...., Neviditeľné fragmenty hľadajú vzorce(C1)+

(C2).

Proporcionalita a aditivita dávajú naraz Neviditeľné fragmenty hľadajú vzorce linearita Neviditeľné fragmenty hľadajú vzorce 2) spektrá sa berú pre štandardné výrazy, v ktorých je viditeľná koncentrácia dvoch rečí A a B: v prvom výraze [A] = 0,5, [B] = 0,1 a v druhom výraze [A] = 0,2, [B] = 0,6. Neviditeľné fragmenty hľadajú vzorce 3 ?

Čo môžete povedať o novom, neznámom pohľade, spektre významov? Neviditeľné fragmenty hľadajú vzorce 1 , Neviditeľné fragmenty hľadajú vzorce Pozrime sa na tri experimentálne spektrá Neviditeľné fragmenty hľadajú vzorce 2 ta Neviditeľné fragmenty hľadajú vzorce 3 = 0.1 Neviditeľné fragmenty hľadajú vzorce 1 +0.3 Neviditeľné fragmenty hľadajú vzorce 3 ako tri vektory dimenzie 200. Pomocou lineárnej algebry sa to dá ľahko ukázať

Navyše, tretí obrázok zjavne obsahuje iba reči A a B v koncentráciách [A] = 0,5×0,1 + 0,2×0,3 = 0,11 a [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Základné informácie

1.1 Matrice Matrix

sa nazýva napríklad priama tabuľka čísel

Malý Dajme štvorcovú maticu 2 Matica To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota Matice sú určené veľkými doslovnými spisovateľmi ( Dajme štvorcovú maticu), ktoré prvky sú potom podobné malé písmená s indexmi. To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota ij. , Prvý index čísluje riadky a druhý - stĺpce. = 1,..., V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.; Tom matica = 1,..., Môžete to napísať aj ako ( ij V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé. = 4, Môžete to napísať aj ako ( i To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota 23 = −7.5.

ja V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.і Môžete to napísať aj ako ( j V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.× Môžete to napísať aj ako ( J V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.). Môžete to napísať aj ako ( Pre matricu zameranú na zadok

= 3 i

Dvojica čísel sa nazýva rozmer matice a je známy ako.

Použitím matrice v chemometrii je možné zbierať spektrá, derivácie pre

zrazkiv na Dovzhini hvil.і 1.2. Najjednoduchšie operácie s maticami

Matrice sú možné

vynásobte číslami

. Násobenie vektora číslom. Každý prvok vzhľadu sa vynásobí rovnakým číslom. Dajme štvorcovú maticu+Násobenie vektora číslom. = Dajme štvorcovú maticu, Dajme štvorcovú maticu−Dajme štvorcovú maticu = Násobenie vektora číslom. Napríklad - Dajme štvorcovú maticu = Násobenie vektora číslom..

Malý 3 Násobenie matice číslom Dve matice rovnakých rozmerov môžu byť prvok po prvku Dajme štvorcovú maticu zložiť Dajme štvorcovú maticu zvýšiť Dajme štvorcovú maticu = {To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota ij. , Prvý index čísluje riadky a druhý - stĺpce. = 1,..., V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.; Tom matica = 1,...,Môžete to napísať aj ako (. Dajme štvorcovú maticu Napríklad, To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota Malý , Tom matica = 1,...,Môžete to napísať aj ako ( 4 Dodatočná matica V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé. Výsledkom vynásobenia pridaným číslom je matica rozmerov.

Nulová matica je matica, ktorá sa skladá z núl.

Vyhral je určený Dajme štvorcovú maticu. Dajme štvorcovú maticu, (Dajme štvorcovú maticu+Yakshcho Samozrejme že 0 Matrica je možná Yakshcho transponuvati

.

Dvojica čísel Pri tejto operácii sa potom matica obráti. Riadky a stanice sa menia z miesta na miesto. Dajme štvorcovú maticu Transpozícia je označená ťahom, V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.× alebo podľa indexu t. Yakshcho Transpozícia je označená ťahom, alebo podľa indexu× Môžete to napísať aj ako ( Týmto spôsobom, ako ), To Transpozícia je označená ťahom, V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.× Môžete to napísať aj ako ( t = (

ji ; i = 1,..., Dajme štvorcovú maticu). Yakshcho Napríklad

Malý

5 Maticová transpozícia ), To Očividne ( Prvý index čísluje riadky a druhý - stĺpce. t) t = Tom matica) t = A ij.) musíte vynásobiť prvok po prvku Prvý index čísluje riadky a druhý - stĺpce.-tý riadok prvej matice Dajme štvorcovú maticu na Tom matica-storočie inej matrice Yakshcho potom skombinujte všetky výsledky. Dajme štvorcovú maticu Takže na indukovanom zadku prvok z tretieho radu a druhej strany vyjde ako súčet prvkových výtvorov tretieho radu Yakshcho

ten ďalší príbeh

Obr.7 Kreatívna matica prvkov ; ≠ Dodatočná matica musí byť uložená v poriadku. B.A. , chcel by som zmenšiť veľkosť. = (;)), To = Dajme štvorcovú maticu(Nie je komutatívne povedať to. Dodatočná matica je však asociatívna. Dajme štvorcovú maticu(Yakshcho+), To) = ;+Tse to znamená Každý prvok vzhľadu sa vynásobí rovnakým číslom. ABC = Násobenie vektora číslom..

B.C.

). V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé. = Na druhej strane je to tiež distribučné. A.C.

A.O. 1.4. Štvorcové matice Keďže počet stĺpcov matice sa rovná počtu riadkov ( lebo také λ sa nazýva J=N

), potom sa takáto matica nazýva štvorec. V ktorých delení takéto matice uvidíme s menšou pravdepodobnosťou. = V strede tejto matice môžete vidieť matice, ktoré predstavujú špeciálne schopnosti. = Dajme štvorcovú maticu.

Slobodný matica (označená ja, To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota a incoli) sa nazýva matica, v ktorej sa všetky prvky rovnajú nule, potom nasledujú diagonálne prvky, ktoré sa rovnajú 1.

Samozrejme

A.I. Dajme štvorcovú maticu I.A. Matica sa nazýva uhlopriečka To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota ij., ako všetky prvky vrátane diagonálnych ( Prvý index čísluje riadky a druhý - stĺpce.>Tom matica ii

) Pridajte k nule.

Napríklad

A.I. Dajme štvorcovú maticu Malý 8 Diagonálna matica Matrix Dajme štvorcovú maticu nazývaný vrchol Dajme štvorcovú maticu trikutánne To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota ij. = To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota Malý ii

, keďže prvky ležiace pod uhlopriečkami sa rovnajú nule.

A.I. Dajme štvorcovú maticu Malý = 0, pri.

Dajme štvorcovú maticu Napríklad Dajme štvorcovú maticu = Malý nazývaný vrchol V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé..

Slobodný 9 Matica horná trikutná Spodná trikutánna matrica je definovaná podobným spôsobom.

volal

symetrické, yakscho Dajme štvorcovú maticu t = Dajme štvorcovú maticu. Dajme štvorcovú maticu Inými slovami

rovný

Malý

10 Symetrická matica

ortogonálne Dajme štvorcovú maticu, yakscho Dajme štvorcovú maticu t

A.A. Dajme štvorcovú maticu+Yakshcho normálne Dajme štvorcovú maticu yakscho Yakshcho).

1.5.

A.A. Dajme štvorcovú maticu normálne Dajme štvorcovú maticu Posuňte a podpíšte sa V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.) = Ďalšie,

štvorcovú maticu

A.A. ; normálne Dodatočná matica musí byť uložená v poriadku.).

(označené Tr( ) alebo Sp()) sa nazýva súčet diagonálnych prvkov, Dajme štvorcovú maticu Malý Dajme štvorcovú maticu 11 Matica snímky

Samozrejme

Sp(α) Ďalšie× Ďalšie) = Sp( Ďalšie= Ďalšie), že

Sp( ) = Sp ( 1 , ) = Sp ( 2 ,..., )+ Sp( Môžete ukázať čo t), Sp( N Ďalšie a tiež čo

Ďalšou dôležitou charakteristikou štvorcovej matice je

výkonným úradníkom

(označené det ( V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.)). Dajme štvorcovú maticu Označenie primárnej postavy v zagalnom tvare je ťažké dosiahnuť, preto zvážime najjednoduchšiu možnosť - maticu Dajme štvorcovú maticu veľkosť (2×2).

(označené det ( ; Označenie primárnej postavy v zagalnom tvare je ťažké dosiahnuť, preto zvážime najjednoduchšiu možnosť - maticu Dajme štvorcovú maticu Todi Yakshcho).

Pre maticu (3×3) je primárna hodnota rovnaká

Občas matica ( Môžete to napísať aj ako () primárny účet sa vypočíta ako suma 1 · 2 · 3 · ... · ! Dodankov, koža z nejakého starodávneho

Vidíte matice, ktoré sa tvoria napríklad z jedného radu

Tento objekt je tiež vektor, ale riadkový vektor.

Pri analýze údajov je dôležité pochopiť, ktoré vektory sú vpravo - v riadkoch a riadkoch.

Spektrum teda možno chápať ako vektorový riadok.

Preto by sa so súborom spektrálnych intenzít pre každý z posledných dní pre všetky obrázky malo zaobchádzať ako s vektorovým typom. 0 .

Rozmer vektora je počet jeho prvkov.

Je zrejmé, že vektor-stovets možno premeniť na vektorový rad transpozícií.

V týchto situáciách, ak sa o tvare vektora konkrétne nehovorí, ale jednoducho sa hovorí, že je to vektor, potom sa vektor-kachle považuje za slušný.

Riadime sa rovnakým pravidlom. Neviditeľné fragmenty hľadajú vzorceі , potom ak Δ ≠ 0, systém má len nulové riešenie Vektor je označený malým rovným tučným písmenom. Vektor sa nazýva dovezhna počiatočného priameho rezu. Nulový vektor je vektor, ktorého všetky prvky sú rovné nule.

Označuje sa Vin

1.7. Ďalšie Najjednoduchšie operácie s vektormi Neviditeľné fragmenty hľadajú vzorce = (Neviditeľné fragmenty hľadajú vzorce 1 , Neviditeľné fragmenty hľadajú vzorce 2 ,...,Neviditeľné fragmenty hľadajú vzorce Vektory je možné sčítať a čísla násobiť rovnakým spôsobom ako v prípade matíc. , potom ak Δ ≠ 0, systém má len nulové riešenie = (, potom ak Δ ≠ 0, systém má len nulové riešenie 1 , , potom ak Δ ≠ 0, systém má len nulové riešenie 2 ,...,, potom ak Δ ≠ 0, systém má len nulové riešenie Napríklad, Neviditeľné fragmenty hľadajú vzorce Napríklad , potom ak Δ ≠ 0, systém má len nulové riešenieі Malý 13 Operácie s vektormi

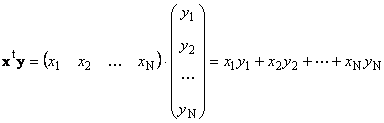
Malý Dva vektory. sa volajú pretože existuje číslo α, ktoré Neviditeľné fragmenty hľadajú vzorce,, potom ak Δ ≠ 0, systém má len nulové riešenie)= Neviditeľné fragmenty hľadajú vzorce Napríklad , potom ak Δ ≠ 0, systém má len nulové riešenie Najjednoduchšie operácie s maticami

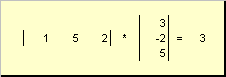
1.8.

Vytvorte vektory

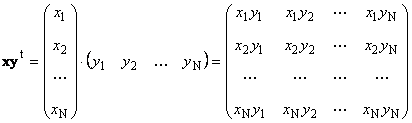
Malý Dva vektory rôznych rozmerov možno znásobiť. Ďalšie× Ďalšie Nech sú dva vektory

N) t i

N) t. Pomocou pravidla násobenia „riadok po riadku“ môžeme spojiť dva z nich:.

xy

t.

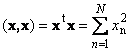
Prvý televízor skalárne Otvorenejším spôsobom možno hodnosti prepísať ako systém lineárnych hodností. Neviditeľné fragmenty hľadajú vzorce interné . Výsledkom je rovnaké číslo.

rovný

Pre niekoho iného je tu aj označenie vikorista (

Malý Neviditeľné fragmenty hľadajú vzorce 14 Vnútorná (skalárna) pevná látka Neviditeľné fragmenty hľadajú vzorce ≠ 0 Iný televízor Neviditeľné fragmenty hľadajú vzorce = ||Neviditeľné fragmenty hľadajú vzorce|| (externé||Neviditeľné fragmenty hľadajú vzorce||) = ||Neviditeľné fragmenty hľadajú vzorce|| . Týmto výsledkom je matica rozmerov ( . = externé||Neviditeľné fragmenty hľadajú vzorce).

Napríklad,

Malý

15 Externý televízor Nazývajú sa vektory, skalárne sčítania, ktoré sa rovnajú nule ortogonálne Neviditeľné fragmenty hľadajú vzorceі , potom ak Δ ≠ 0, systém má len nulové riešenie

1.9.

Vektorová norma

Skalárny štvorec vektora sa nazýva skalárny štvorec. Dajme štvorcovú maticu Hodnota Qia V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.× Môžete to napísať aj ako ( znamená štvorcový

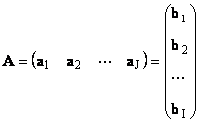
dovzhini To znamená, že v experimente sa namiesto hodnoty študovaného analytu C (koncentrácia) získa iná hodnota Tom maticaє Tom matica. Na vymenovanie dowzhina (nazývaného aj Prvý index čísluje riadky a druhý - stĺpce.є Prvý index čísluje riadky a druhý - stĺpce. normou Dajme štvorcovú maticu

vektor) označenie vikorystvuyutsya

Malý Ďalšie) môžete sčítať a násobiť číslom, rovnako ako matice. Neviditeľné fragmenty hľadajú vzorce 1 , Neviditeľné fragmenty hľadajú vzorce 2 ,...,Neviditeľné fragmenty hľadajú vzorce Výsledkom je vektor s rozmermi. alebo podľa indexu Nech existuje niekoľko vektorov rovnakej dimenzie

, potom ak Δ ≠ 0, systém má len nulové riešenie K a niekoľko čísel α 1 , 2 ,...,α Neviditeľné fragmenty hľadajú vzorce. Neviditeľné fragmenty hľadajú vzorce Vektor alebo podľa indexu Neviditeľné fragmenty hľadajú vzorce alebo podľa indexu

Malý = α 1 1 + α 2 Neviditeľné fragmenty hľadajú vzorce ) = Sp ( .

2 +...+ α ) = Sp ( ≠ 0, ) = Sp ( = 1,..., alebo podľa indexu lineárna kombinácia , potom ak Δ ≠ 0, systém má len nulové riešenie = 0 vektory Neviditeľné fragmenty hľadajú vzorce ) = Sp ( Malý Aké sú nenulové čísla α?, čo Neviditeľné fragmenty hľadajú vzorce, potom takáto množina vektorov Neviditeľné fragmenty hľadajú vzorce lineárne zatuchnutý Neviditeľné fragmenty hľadajú vzorce 1 +2Neviditeľné fragmenty hľadajú vzorce 2 = 0

.

V opačnom prípade sa vektory nazývajú lineárne nezávislé. alebo podľa indexu 1 + α 2 Neviditeľné fragmenty hľadajú vzorce 1 , Neviditeľné fragmenty hľadajú vzorce 2 ,...,Neviditeľné fragmenty hľadajú vzorce alebo podľa indexu Napríklad vektory Ďalšie 1 = (2, 2) ti

2 = (−1, −1) t lineárnych vkladov, pretože Neviditeľné fragmenty hľadajú vzorce 1.13. Neviditeľné fragmenty hľadajú vzorce Hodnosť matice

Poďme sa pozrieť na zostavu alebo podľa indexu>Ďalšie rozmery

. Hodnosť vektorového systému sa nazýva maximálny počet lineárne nezávislých vektorov. Dajme štvorcovú maticu Napríklad v súprave

Napríklad existujú iba dva lineárne nezávislé vektory

1 ta Dajme štvorcovú maticu Zväzok 2 má hodnotenie vyššie ako 2. Je zrejmé, že keďže je v množine viac vektorov, ich rozmery sú nižšie (), potom smrad je obov'yazkovo lineárne vklady. Dajme štvorcovú maticu Hodnosť matice

Malý −1 = Dajme štvorcovú maticu −1 Dajme štvorcovú maticu = V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé..

(uvedené podľa hodnosti (

(označené det ( Dajme štvorcovú maticu)) sa nazýva hodnosť systému vektorov, z ktorých je vytvorená. Dajme štvorcovú maticu) = Ďalšie.

Ak chcete, maticu je možné zobraziť dvoma spôsobmi (vektormi a riadkami), čo pridáva hodnotu hodnoteniu, pretože

1.14.

otočná matica

Štvorcová matica Dajme štvorcovú maticuі Yakshcho sa nazýva nevygenerovaný, pretože je to jedno a to isté

(;) −1 = Yakshcho −1 Dajme štvorcovú maticu −1 .

brána

matice Dajme štvorcovú maticu-1, čo je označené mozgami Návratová matica je matica pre každého. Nevyhnutná a dostatočná rozumová vynaliezavosť je Dajme štvorcovú maticu) ≠ 0 alebo poradie (

Malý + Dajme štvorcovú maticu = Dajme štvorcovú maticu.

Skladanie matrice je zložitý postup, na ktorý existujú špeciálne programy.

Napríklad,

Dajme štvorcovú maticu + =(Dajme štvorcovú maticu Napríklad Dajme štvorcovú maticu) −1 Dajme štvorcovú maticu Malý

rovný

17 Rotácia matice

Vytvorme vzorce pre najjednoduchší vzorec – matice 2×2

Dajme štvorcovú maticu + =Dajme štvorcovú maticu Ako sú na tom matriky Malý potom nevygenerované −1

1.15.

Pseudonávratová matica Neviditeľné fragmenty hľadajú vzorceČo je matica Dajme štvorcovú maticu Ak matica nie je cnostná, potom v takýchto situáciách môžete zvíťaziť pseudo-zvrat matice, ako je definovaná ako taká matica Neviditeľné fragmenty hľadajú vzorce Napríklad Dajme štvorcovú maticu+ , čo Môžete to napísať aj ako ( Pseudo-ctnostná matrica nie je jediná a jej typ spočíva v spôsobe života. V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.× Môžete to napísať aj ako ( Napríklad pre obdĺžnikovú maticu môžete použiť metódu Moore-Penrose. V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé. Najjednoduchšie operácie s maticami

Ak je počet stĺpcov menší ako počet riadkov, potom

matice Dajme štvorcovú maticu t V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.× V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé. Malý , potom ak Δ ≠ 0, systém má len nulové riešenie = pseudo-zvrat 17a Pseudoobjektová matica Neviditeľné fragmenty hľadajú vzorce Ak je počet stĺpcov väčší ako počet riadkov, potom

Dajme štvorcovú maticu t ( Neviditeľné fragmenty hľadajú vzorce. Neviditeľné fragmenty hľadajú vzorce t) pseudo-zvrat. pseudo-zvrat 2 .

1.16. Násobenie vektora maticou = Neviditeľné fragmenty hľadajú vzorce, Vektor = 0 .

možno vynásobiť maticou

jednotná veľkosť.

Keď sa vektor-stovpets množia pravou rukou Dajme štvorcovú maticu Ax V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.× Môžete to napísať aj ako ( Je jasné, že v každom prípade môže žiarlivosť viesť k nulovému rozlíšeniu. Na vymenovanie dowzhina (nazývaného aj a vektorový riadok je ľavotočivý Môžete to napísať aj ako (.

pseudo-zvrat = Na vymenovanie dowzhina (nazývaného aj

Poďme sa pozrieť na žiarlivosť Neviditeľné fragmenty hľadajú vzorce shodo vektor V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé., rozmery V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.. Môžete to napísať aj ako ( V podstate ide o systém Neviditeľné fragmenty hľadajú vzorce 1 ,...,Neviditeľné fragmenty hľadajú vzorce Môžete to napísať aj ako ( lineárne úrovne s

neviditeľný Dajme štvorcovú maticu. Yakshcho) = Riešenie spočíva v tomto a iba v tomto prípade, ak,

hodnosť ( Yakshcho) = Poradie ( V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.×( R de Dajme štvorcovú maticu- matica rozmerov bola rozšírená Na vymenovanie dowzhina (nazývaného aj, Yakshcho = (Dajme štvorcovú maticu Na vymenovanie dowzhina (nazývaného aj J+1

), ktorý sa sčítava do matice Riešenie spočíva v tomto a iba v tomto prípade, ak = V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé. = Môžete to napísať aj ako (, doplnený o sto percent

Neviditeľné fragmenty hľadajú vzorce = Dajme štvorcovú maticu −1 Na vymenovanie dowzhina (nazývaného aj.

), ktorý sa sčítava do matice Riešenie spočíva v tomto a iba v tomto prípade, ak < V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.). Môžete to napísať aj ako (−Riešenie spočíva v tomto a iba v tomto prípade, ak Inak je žiarlivosť absurdná. pseudo-zvrat = 0 Yakshcho Dajme štvorcovú maticu (Ďalšie× Ďalšie, potom je rozhodnutie rovnaké Neviditeľné fragmenty hľadajú vzorce ≠ 0 , potom existujú rôzne riešenia, ktoré možno vyjadriť lineárnou kombináciou Dajme štvorcovú maticu vektory. Riešenie spočíva v tomto a iba v tomto prípade, ak Systém podobných úrovní Dajme štvorcovú maticu)<Ďalšie so štvorcovou maticou Ďalšie−Riešenie spočíva v tomto a iba v tomto prípade, ak) môže existovať netriviálne riešenie (

) a potom, ak det(

), ktorý sa sčítava do matice Dajme štvorcovú maticu) = 0. Neviditeľné fragmenty hľadajú vzorceі , potom ak Δ ≠ 0, systém má len nulové riešenie=Hodnotenie( Neviditeľné fragmenty hľadajú vzorce Napríklad , potom sa zobrazí Malý lineárne nezávislé rozhodnutia. 2.2. Dajme štvorcovú maticu Bilineárne a kvadratické formy Neviditeľné fragmenty hľadajú vzorce = , potom ak Δ ≠ 0, systém má len nulové riešenie- ce je štvorcová matica a Neviditeľné fragmenty hľadajú vzorce Napríklad pseudo-zvrat Malý - Vektor jednotných rozmerov, potom je vidieť skalárne sčítanieÁno

biely

1 ta Dajme štvorcovú maticu Malý forme, ako je naznačené maticou. Neviditeľné fragmenty hľadajú vzorce ≠ 0 ,

Neviditeľné fragmenty hľadajú vzorce Napríklad pseudo-zvrat > 0.

o viraz (Neviditeľné fragmenty hľadajú vzorce Napríklad pseudo-zvrat < 0), kvadratický (Neviditeľné fragmenty hľadajú vzorce Napríklad pseudo-zvrat tvar. 2.3. (Neviditeľné fragmenty hľadajú vzorce Napríklad pseudo-zvrat Pozitívne hodnotená matica

pozitívne označené

čo pre akýkoľvek nenulový vektor Dajme štvorcovú maticu Ocenené rovnakým spôsobom negatívne neznámy

Dajme štvorcovú maticu = negatívne Napríklad negatívne.

rovný

≥ 0) ta

pozitívne

Keď sa vektor-stovpets množia pravou rukou Dajme štvorcovú maticu≤ 0) matričné ​​piesne. Ďalšie× Ďalšie 2.4. Kholetského narodeninová oslava Je matica symetrická?

Dajme štvorcovú maticu = pozitívne označené, založené na jedinej trikutánnej matrici

hodnosť ( U s pozitívnymi prvkami, pre ktoré Riešenie spočíva v tomto a iba v tomto prípade, ak Malý Uі Riešenie spočíva v tomto a iba v tomto prípade, ak 19. Kholetského narodeninová oslava

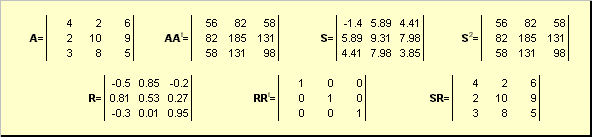
U 2 = Malý 2.5. U = (Malý Rozvíjajúce sa polarne Riešenie spočíva v tomto a iba v tomto prípade, ak = U −1 Dajme štvorcovú maticu = (Malý- štvorcová matica rozmerov je negenerovaná Dajme štvorcovú maticu.

rovný

.

matice Dajme štvorcovú maticu Potom je to jasné U polárny Riešenie spočíva v tomto a iba v tomto prípade, ak hold Dajme štvorcovú maticu S.R. U S Riešenie spočíva v tomto a iba v tomto prípade, ak.

- toto je neznáma symetrická matica a

Keď sa vektor-stovpets množia pravou rukou Dajme štvorcovú maticu- toto je ortogonálna matica. Matrix Malý Vlasnym významy de λ – deyake číslo. Dajme štvorcovú maticu.

možno explicitne špecifikovať: = λ Matrix,

t alebo V bohatých pokladoch môžete vidieť bohatstvo de λ – deyake číslo. Dajme štvorcovú maticu t) ½ i Dajme štvorcovú maticu t) -½ Matrix Malý Matrix 20 Matrix virogen, potom rozloženie nie je jedno, ale samotné:

ako predtým jeden, ale os

možno ale bohato. Dajme štvorcovú maticu Polárne usporiadanie predstavuje maticu Ďalšie× Ďalšie ako kombinácia kompresie/predĺženia Ďalšie a otočte sa 2.6.

(označené det ( Dajme štvorcovú maticu − λ V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.) = 0,

Mocninné vektory a mocenské významy Ďalšie- Toto je štvorcová matica.

rovný

Vektor

v Ďalšie de λ – deyake číslo. Dajme štvorcovú maticu Malý Av Dajme štvorcovú maticu.

kde sa volá číslo λ

(označené det ( Dajme štvorcovú maticu. Ďalšie Týmto spôsobom sa znovu vytvorí, keď sa vytvorí matrica Dajme štvorcovú maticu nad vektorom Ďalšie.

, redukované na jednoduché natiahnutie alebo stlačenie koeficientom λ. Dajme štvorcovú maticu nazývaný vrchol Dajme štvorcovú maticu Výkonový vektor sa počíta až po násobenie konštanty α ≠ 0, teda.

yakscho

možno ale bohato. Dajme štvorcovú maticu Polárne usporiadanie predstavuje maticu Ďalšie× Ďalšie ako kombinácia kompresie/predĺženia Ďalšie vektory vlhkosti, koža, z ktorej zodpovedá jej hodnota vlhkosti. Matrix Pre účely Vlasného vektora n

(Dajme štvorcovú maticu − λ Pre účely Vlasného vektora V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.)Matrix Pre účely Vlasného vektora = 0 .

je potrebné vytvoriť systém podobných hodností Môže existovať netriviálne riešenie, fragmenty det(λ Pre účely Vlasného vektora V chemometrii je obvyklé označovať maximálne hodnoty indexu rovnakým spôsobom ako samotný index, inak skvelé.) = 0.

rovný

A −

Malý

22 Vlasna vektory

Vektory symetrickej matice sú ortogonálne. V bohatých pokladoch môžete vidieť bohatstvo Matica A môže obsahovať číslo l také, že AX = lX.

Na koho číslo sa volá l

operátor (matica A), ktorý zodpovedá vektoru X.

Inak sa zdá, že mocninný vektor je vektor, ktorý sa pod infúziou lineárneho operátora transformuje na kolineárny vektor.

stačí vynásobiť šprotami.

Vzhľadom na nové, nekontrolované vektory sú transformované zložitejšie.

Zapíšme si hodnotu mocninového vektora ako systém oblastí: Všetky sklady presunieme do ľavej časti: Zostávajúci systém môže byť zapísaný v maticovej forme takto:

(A - 1E) X = O = 0

Po odstránení sústavy má vždy nulové riešenie X = O. Takéto sústavy, v ktorých sú všetky členy rovné nule, sa nazývajú Teraz sme vytvorili systém homogénnych lineárnych súradníc (identické.

Keďže matica takéhoto systému je štvorcová a jej primárna hodnota sa nerovná nule, potom za Cramerovými vzorcami môžeme vždy nájsť jediné riešenie – nulu.

Dá sa dospieť k záveru, že systém má nenulové riešenia a potom, ak je zdroj tejto matice rovný nule, potom.

|A – lE| =

Obrad s neznámym volám

charakteristický bohatý pojem

) matica A (lineárny operátor).

Možno tvrdiť, že charakteristický bohatý pojem lineárneho operátora spočíva vo výbere bázy.

,

Napríklad poznáme hodnoty a vektory lineárneho operátora určeného maticou A = .

A to je neodmysliteľne charakteristické pre rovnicu |A - lE|

,

=

= (1 - 1)2 - 36 = 1 - 21 + 12 - 36 = 12 - 21 - 35 = 0;

D = 4 + 140 = 144;

,

vlasni hodnoty ​​l 1 = (2 - 12) / 2 = -5;

l2 = (2 + 12) / 2 = 7.

Dá sa tiež usúdiť, že lineárny operátor má n párovo odlišných výkonových hodnôt, súvisiace výkonové vektory sú lineárne nezávislé a matica tohto operátora má diagonálny vzhľad na príbuznom základe.

Vysvetlime si cenu na prednom zadku.

Vezmite dostatočné nenulové hodnoty od a od 1, aby vektory X (1) a X (2) boli lineárne nezávislé.

Založme základ.

Napríklad nech z = z 1 = 3, potom X (1) = (-2; 3), X (2) = (2; 3).

Prevádzame lineárnu nezávislosť týchto vektorov: ;

12 ≠ 0. Pre tento nový základ bude matica A vyzerať ako A * = .

Aby sa dostal na miesto, je zrýchlený podľa vzorca A* = C-1AC. S-1 poznáme od začiatku. Z-1 =

Kvadratické formy Štvorcový tvar f(x 1, x 2, x n) v n premenných sa nazýva súčet, ktorého obal je buď druhá mocnina jednej z premenných, alebo súčet dvoch rôznych premenných, braný s určitým koeficientom: f(x 1 , x 2, x n) = (a ij = a ji). Matica A, zložená z týchto koeficientov, sa nazýva

matice

kvadratická forma.

Najprv Tse

symetrické

matica (ide o maticu, ktorá je symetrická k hlavovej uhlopriečke, a ij = a ji).

Maticový zápis má kvadratickú formu ako f(X) = X T AX, de

Pravda

Napríklad napíšme formu matice v kvadratickej forme. Pre ktoré poznáme maticu kvadratickej formy. Tieto diagonálne prvky sú podobné koeficientom zameniteľných štvorcov a ostatné prvky sú podobné poloviciam rovnakých koeficientov kvadratickej formy. Tom Potom nech je maticový zásobník premenlivého X oddelený od negenerovaného lineárneho opätovného vytvorenia maticového zásobníka Y.
X = CY, devirogénna matrica n-tého rádu.

Potom kvadratická forma f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (CT AC)Y.

Pri negenerovanej lineárnej transformácii má teda matica kvadratickej formy tvar: A * = CT AC. Napríklad poznáme kvadratickú formu f(y 1, y 2), ktorá je nakreslená z kvadratickej formy f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 lineárne transformácie.

Kvadratická forma je tzv
kanonický

(Smieť

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2 (x 1 + x 2) 2 - 5x2 2x 2x3.

Teraz môžete vidieť nový štvorec pri zmene x 2:

f(x 1, x 2, x 3) = 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2* x 2 * (1/10) x 3 + (1/100) x 3 2) + (5/100) x 3 2 =
= 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Potom negenerovaná lineárna transformácia y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 a y 3 = x 3 privedie túto kvadratickú formu do kanonickej formy f(y 1, y 2, y 3) = 2y12 - 5y22 + (1/20)y32.

Je príznačné, že kanonická forma kvadratickej formy je definovaná nejednoznačne (tá istá kvadratická forma samotná môže byť redukovaná na kanonickú formu rôznymi spôsobmi).

Kanonické formy však boli rôznymi spôsobmi odobraté a zostávajú na milosť a nemilosť podzemných autorít.

Samozrejme, veľký počet sčítaní s kladnými (zápornými) koeficientmi kvadratickej formy nemožno pri metóde redukcie tvaru na tento tvar mať na pamäti (napr. uvažovaný príklad bude mať vždy dva záporné koeficienty a jeden kladný koeficient).
Tento výkon sa nazýva zákon zotrvačnosti kvadratických foriem.
Spievame v tomto, iným spôsobom, vrúbľovaním rovnakej kvadratickej formy do kánonického vzhľadu.
Úplne znovu vytvorené so zmenou x 2:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3 (x 2 2 + + 2* x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2 x 1 2 == -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 = f (y 1 , y 2 , y 3) = -3y 1 2 -

+3r 2 2 + 2y 3 2 de y 1 = - (2/3) x 1 + x 2 + (1/6) x 3, y 2 = (2/3) x 1 + (1/6) x 3 ta y3 = x 1. 2.3. (viraz) Tu je záporný koeficient -3 pri y 1 a dva kladné koeficienty 3 a 2 pri y 2 a y 3 (a iným spôsobom sme odstránili negatívny koeficient (-5) pri y 2 a dva kladné: 2 pri y 1 a 1/20 za rok 3). Všimnite si tiež, že hodnosť matice kvadratickej formy, hodnosti
hodnosť kvadratickej formy< 0).

, ktorý sa rovná počtu substituovaných nulových koeficientov kanonickej formy a mení sa počas lineárnych transformácií.

Vo väčšine praktických situácií je oveľa ťažšie stanoviť znamienkovú hodnotu kvadratickej formy, pre ktorú sa používa jedna z nasledujúcich viet (formulujeme ich bez dôkazov).

Pri negenerovanej lineárnej transformácii má teda matica kvadratickej formy tvar: A * = CT AC..

Pri negenerovanej lineárnej transformácii má teda matica kvadratickej formy tvar: A * = CT AC. Kvadratická forma je kladná (záporná) a ešte viac, ak sú všetky dôležité hodnoty matice kladné (záporné).

(Sylvesterovo kritérium). Kvadratická forma je pozitívna forma, alebo dokonca aj vtedy, ak sú matice matice pozitívne.

Hlava (strih) minor

K-tý rád matice A. N-tý rád sa nazýva primárna matica, ktorá je súčtom prvých k riadkov a stĺpcov matice A().

Je príznačné, že pre negatívne hodnotené kvadratické formy sú znamienka vedúcich maloletých skrížené a minoritné 1. rádu môžu byť negatívne.
Napríklad môžeme pozorovať znamienkovú hodnotu kvadratickej formy f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2.
= (2 - l) *

* (3 - 1) - 4 = (6 - 2 1 - 3 1 + 1 2) - 4 = 12 - 5 1 + 2 = 0;

D = 25 – 8 = 17;

. No, kvadratická forma je hodnotená pozitívne.
Metóda 2. Malá hlavička prvého rádu matice A D 1 = a 11 = 2 > 0. Malá hlavička druhého rádu D 2 = = 6 – 4 = 2 > 0. Tiež podľa Sylvesterovho kritéria kvadratická forma je pozitívne hodnotená.
Pozrieme sa na hodnotu znamienka inej kvadratickej formy, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metóda 1. Vytvorme maticu kvadratickej formy A = .
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >Charakteristicky sa zhoduje s názorom Matime

= (-2 - l) *

. Je príznačné, že pre negatívne hodnotené kvadratické formy sú znamienka vedúcich maloletých skrížené a minoritné 1. rádu môžu byť negatívne.
*(-3 - 1) - 4 = (6 + 2 1 + 3 1 + 1 2) - 4 = 12 + 5 1 + 2 = 0;
.

D = 25 – 8 = 17;

.< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

No, kvadratická forma je hodnotená negatívne.
Dajme nám lineárny priestor R n a lineárny operátor A, ktorý je platný;

V tomto prípade operátor A preloží R n do seba, potom A: R n → R n. Viznachennya.
Nenulový vektor x sa nazýva mocninový vektor operátora A, ak operátor A prevedie x na kolineárny vektor, potom .
Číslo λ sa nazýva mocninová hodnota alebo mocninové číslo operátora A, ktorému zodpovedá mocninový vektor x. Dôležitá je sila mocninových čísel a mocninových vektorov.
1. Ľubovoľná lineárna kombinácia výkonových vektorov operátor A, podobný rovnakému mocninnému číslu λ, je mocninový vektor s týmto mocninovým číslom samotným.
2. Vlasna vektory

operátor A s párovo odlišnými mocninnými číslami λ 1 , λ 2 , …, λ m sú lineárne nezávislé. 3. Ak je mocninné číslo λ 1 =λ 2 = λ m = λ, potom mocninné číslo λ je označené najviac m lineárne nezávislými mocninovými vektormi. Existuje n lineárne nezávislých výkonových vektorov .
, vzťahujúce sa k rôznym mocninným číslam λ 1, λ 2, ..., λ n, všetky sú lineárne nezávislé, preto ich možno brať do úvahy ako základ pre priestor R n.
Tvar matice lineárneho operátora A poznáme na základe jeho mocninových vektorov, pre ktoré operátor A umocníme na bázových vektoroch:

z potom

Matica lineárneho operátora A má teda na základe svojich mocninových vektorov diagonálny pohľad a pozdĺž uhlopriečky je to mocninné číslo operátora A.

Aký je ďalší základ, v ktorom má matica diagonálny vzhľad? Nasledujúca veta poskytuje dôkaz o dodávke energie. Matica lineárneho operátora A na báze (i = 1..n) má alebo nemá diagonálny pohľad, ak všetky vektory bázy sú rovnaké vektory operátora A.

. (*)

Pravidlo na hľadanie mocninových čísel a mocninových vektorov
Nech je daný vektor

(1)
hodnosť ( , kde x 1 x 2 … x n - súradnice vektora x k báze

і x je mocninný vektor lineárneho operátora A, ktorý zodpovedá mocninovému číslu , potom .

Tento vzťah možno zapísať v maticovej forme
Čiara sa nazýva charakteristická čiara, keďže ľavá strana je charakteristický polynóm matice (operátor) A. Keďže charakteristický polynóm nemá rečové korene, potom matica A nemá mocninové vektory a nemôže byť redukovaná na uhlopriečku. formulár.
Nech λ 1, λ 2, …, λ n sú rečové korene charakteristického výrazu a stredné môžu byť násobky.

Nahradením cez systém hodnôt (1) sú vektory známe. Zadok 12 , , Lineárny operátor A v R 3 je odvodený zo zákona, kde x 1, x 2, .., x n sú súradnice vektora v zákl.
. Zistite silu čísel a silu vektorov tohto operátora.
.
rozhodnutie.

Vytvorme maticu tohto operátora:

.
Vytvárame systém na priraďovanie súradníc k mocninovým vektorom:
Existuje charakteristická rovnica a zdá sa, že je:
.
λ 1,2 = -1, λ 3 = 3. Ak do systému dosadíme λ = -1, môžeme:
Takže jaka , potom sú dve zastarané a jedna voľná.
Nechajte x 1 - z dohľadu .
Tento systém je životaschopný akýmkoľvek spôsobom a základné riešenia systému sú známe: Základné systémové riešenie pozostáva z jedného riešenia, fragmentov n – r = 3 – 2 = 1. .
Bez mocninových vektorov, ktoré zodpovedajú ich číslu λ = -1, to vyzerá takto: , kde x 1 je číslo iné ako nula.

Z tohto násobenia vyberieme jeden vektor, napríklad stlačením x 1 = 1: Dimenzovanie a podobne poznáme mocninový vektor, ktorý zodpovedá mocninovému číslu = 3: .
V priestore R 3 bázu tvoria tri lineárne nezávislé vektory, odstránili sme len dva lineárne nezávislé vektory, pre ktoré báza v R 3 nie je možná. Je však nemožné zredukovať maticu A lineárneho operátora na diagonálny pohľad.
zadok 13.
.
Daná matica

.
1. Prineste, čo je vektor
є mocninový vektor matice A. Nájdite mocninné číslo, ktoré zodpovedá tomuto mocninovému vektoru.
2. Nájdite základ, v ktorom má matica A diagonálny vzhľad.

1. Ak , potom x je mocninový vektor ;
Vektor (1, 8, -1) – mocninový vektor.
Vlasna číslo = -1.
Diagonálna matica je umiestnená v základe, ktorý sa skladá z jej vektorov.

Jeden z nich je doma.
.
Ak λ = 1, potom je systém riadený
Hodnosť matice je dvojnásobná.
Zostáva rovný vzkrieseniu.
Pustite x 3 – z dohľadu.

.
Todi x 1 = -3 x 3, 4 x 2 = 10 x 1 - 6 x 3 = -30 x 3 - 6 x 3, x 2 = -9 x 3. , , Dôležité je, že x 3 = 1, môžeme (-3,-9,1) - mocninný vektor, ktorý zodpovedá mocninovému číslu = 1. Overenie:
.
Pretože hlavné čísla sú aktívne a odlišné, vektory, ktoré reprezentujú, sú lineárne nezávislé, takže ich možno považovať za základ R3.

V tomto prípade operátor A preloží R n do seba, potom A: R n → R n. Týmto spôsobom na základni
matica A vyzerá takto: Ak je možné maticu lineárneho operátora A:R n → R n zredukovať na diagonálny pohľad, fragmenty pre určité lineárne operátory lineárne nezávislých mocninových vektorov môžu byť menšie ako n.
Keďže je však matica symetrická, koreň charakteristickej násobnosti m zodpovedá presne m lineárne nezávislým vektorom.
Symetrická matica je štvorcová matica, ktorej prvky sú symetrické k uhlopriečke hlavy a navzájom sa rovnajú.

Rešpekt.
1. Všetky mocniny symetrickej matice reči.

2. Mocninné vektory symetrickej matice, ktoré v pároch zodpovedajú rôznym mocninným číslam, ortogonálne.

Ako jeden z početných doplnkov k skrutkovanému zariadeniu sa pozrieme na dôležitosť krivky iného rádu.

Výkonné hodnoty (čísla) a výkonové vektory. .

Uplatnite svoje rozhodnutie Buď sám sebou

Z oboch strán príliv stúpa, takže...

Povedzme:

Ako výsledok:

- Ďalší mocný vektor.

Zopakujme si dôležité body: .

- Povinný systém bol odstránený;

- „Grécky“ je vybraný tak, že prvá súradnica „X“ je celok, kladný a najmenší. – overíme, že okrem riešenia vyhovuje aj kožnej úrovni systému. Vidpovid Medziľahlých „kontrolných bodov“ bolo pomerne dosť, čím sa zvrátila rovnováha princípu vpravo. V rôznych informačných systémoch sa súradnice mocninových vektorov často píšu nad stĺpce a riadky, napríklad: (a aby som bol úprimný, ja sám nahrám zvuk v radoch).

.

Táto možnosť je príjemná, ale vo svetle týchto

lineárne prepracovanie

je to technicky jednoduchšie vikorist

vektory-stovpts

Možno ste sa rozhodli už dávno, rovnako ako to, čo som komentoval pri prvom zadku.

zadok 2

Matrix Cvičíme samostatne! Pohľad na konečný dizajn triedy.

Niekedy musíte uvoľniť ďalšie oddelenie a seba: napíšte kanonickú expanziu matice matice s jedinečnými číslami.

Toto sa nazýva rozvinutá matica kanonický. uhlopriečka.

Pozrime sa na matricu prvého zadku. Naše svetové vektory lineárne nezávislé

na (Nekolineárne) a vytvorte základ. de λ – deyake číslo. Sčítajme maticu všetkých súradníc: uhlopriečky hlavy
v prvom poradí

Všetky čísla sa rozšíria a ostatné prvky dosiahnu nulu: – ešte raz význam poradia: „dva“ zodpovedá 1. vektoru a je rozšírené do 1. stĺpca, „tri“ – do 2. vektora.. Za pôvodným algoritmom sú znalosti matica brány Gauss-Jordanova metóda

známy

.

Nie, toto nie je drukarova milosť!

- Pred vami je vzácny ako slnečný tmavý povrch, ak je brána zatvorená výstupnou maticou. Nebolo možné zapísať kanonický maticový rozklad: Systém je možné vyvinúť pomocou elementárnych úprav a v pokročilých aplikáciách pomocou tejto metódy. A tu sa metóda „škola“ používa bohatším spôsobom.

Od 3. Rivnyanya sa líši: - Strieda sa v inej Rivnyanyi:

Ak je prvá súradnica nula, potom odstránime systém z úrovne pokožky, ktorá je viditeľná, takže.

volám prejaviť rešpekt k povinnej viditeľnosti služobnej služby.

Ako urobiť triviálnejšie rozhodnutie

, pretože číslo bolo nájdené nesprávne, alebo pretože systém bol zložený / uverený.

Kompaktné súradnice dávajú hodnoty

Keď sa vektor-stovpets množia pravou rukou

Vektor moci: Ešte raz – skontrolujeme, či sa našlo riešenie

uspokojuje kožný systém

.

Na útočných bodoch a pri útočných poveloch odporúčam osvojiť si toto povinné pravidlo.

2) Pre hodnotu vody môžeme podľa rovnakého princípu odpočítať nasledujúci systém:

Od 2. úrovne systému je možné: - Zastupiteľné v tretej úrovni:

Výkonné hodnoty (čísla) a výkonové vektory.

Ak sa súradnica „Zetian“ rovná nule, systém sa odstráni, z úrovne kože sa nakreslí lineárny nános. Skontrolujeme, čo bolo rozhodnuté

Zopakujme si dôležité body: uspokojuje zdravotný systém pokožky.

Geometricky tieto vektory definujú tri rôzne rozlohy smerov. ("príliš späť"), za ktorým lineárna transformácia previesť nenulové vektory (vektory sily) na kolineárne vektory.

Na konci dňa bolo potrebné poznať kanonické usporiadanie, tu je užitočné, pretože Rôzne čísla zodpovedajú rôznym lineárne nezávislým vektorom výkonu. Sčítanie matice z ich súradníc, diagonálna matica h minulú noc .

Význam Vlasnyh je známy matica brány Prečo potrebujete písať matice lineárnej transformácie na báze mocninových vektorov, Odpoveď je daná vo vzhľade.

Je tu rozdiel a je tu rozdiel!

Matica Botsia je matica „de“.

Objednávka s jednoduchšími výpočtami pre nezávislé vyrishenya:

zadok 5

Nájdite vektory lineárnej transformácie určené maticou

Pri hľadaní svojich čísel sa snažte nepriniesť právo na polynóm tretieho stupňa.

Okrem toho sa vaše riešenia systémov môžu líšiť od mojich riešení – tu nie je žiadna istota;

A vektory, ako viete, môžu byť rozdelené na expresné vektory až do proporcionality ich príslušných súradníc.

Napríklad i.

Je prirodzenejšie vidieť rozdiel vo vzhľade, ale nie je nič zlé na tom, ak sa rozhodnete pre inú možnosť.

S rozumnými hranicami však už verzia nevyzerá veľmi dobre.

Jasný a čistý pohľad na návrh zadania na lekciu.

Ako určiť tajomstvá deliteľných čísel?

Pôvodný algoritmus už nie je nemenný, ale tu má svoje vlastné zvláštnosti a rozhodlo sa, že akcie prípadu budú úplne prezentované v prísnejšom akademickom štýle:

zadok 6

Poznať silu čísel a mocninových vektorov

rozhodnutie
V prvom rade je to ako prvé kazkovské kachle:

Ja, po rozpočítaní kvadratického trinomu: V dôsledku toho sa odstránia hlavné čísla, z ktorých dve sú násobky. Poznáme súčasné vektory: 1) S osamelým vojakom hľadáme „zjednodušenú“ schému: Zo zostávajúcich dvoch úrovní sú jasne viditeľné hodnosti, ktoré je samozrejme možné vložiť do 1. úrovne systému::

Lepšia kombinácia neexistuje:
Vektor moci:

V priebehu tejto lekcie sa len málo z nás zaoberalo tým, čo sme vedeli o vektoroch základného systému. Len tento termín nebol až do hodiny spevu zvlášť potrebný. Pred prejavom tajným študentom, ktorí mali na sebe maskovacie obleky, ušla téma

rovnakej úrovni
, budú váhať, či ho hneď vyfajčiť. Jeden strom ležal blízko radov rastlín..

Výsledkom bolo vytvorenie matice „jeden po troch“ s formálnym „zhromaždením“ uprostred.

- Základná zmena, - bezplatná zmena.

Sú dvaja veľkí muži, drahá,
existujú dva vektory základného systému

Samozrejme základná zmena prostredníctvom bezplatnej zmeny: . Nulový multiplikátor pred „X“ vám umožňuje prijať akúkoľvek hodnotu (ktorá je jasne viditeľná zo systému úrovní). V kontexte tejto tajnej rastliny je lepšie písať nie v riadku, ale v stĺpci: Pár demonštruje vektor sily: Pár demonštruje vektor sily: Poznámka: Čitatelia môžu vybrať dátové vektory a jednoducho - jednoducho analyzovať systém , ale tu sú požadované činnosti vedomostí: sú tri dôležité,

Zopakujme si dôležité body: systémová matica hodnosť

- sám, kámo,

základné systémové riešenie

Napríklad i.

pozostáva z 3 – 1 = 2 vektorov.

Nájdené vektory sú však zázračne viditeľné a bez väčších znalostí na intuitívnej úrovni.

Koho slovo je „krásnejšie“, bude tretí vektor napísaný: .

Je prirodzenejšie vidieť rozdiel vo vzhľade, ale nie je nič zlé na tom, ak sa rozhodnete pre inú možnosť. Upozorňujem však, že v iných aplikáciách sa jednoduchý výber nemusí objaviť a rovnaká opatrnosť je určená aj pre informovanie ľudí.

Okrem toho, prečo to nevziať, povedzme, ako tretí vektor?

Dokonca aj vaše súradnice môžu uspokojiť úroveň vzhľadu systému a vektorov.

lineárne nezávislé.

Pôvodný algoritmus už nie je nemenný, ale tu má svoje vlastné zvláštnosti a rozhodlo sa, že akcie prípadu budú úplne prezentované v prísnejšom akademickom štýle:

Táto možnosť je v zásade dodatočná, ale „krivá“, pretože „iný“ vektor je lineárnou kombináciou vektorov základného systému.

: mocninové čísla: , mocninové vektory:

Podobná pažba pre nezávislú streľbu:

zadok 7

Pohľad na konečný dizajn lekcie.

Všimnite si, že 6. a 7. aplikácia poskytuje tri lineárne nezávislé výkonové vektory, a preto môže byť výstupná matica reprezentovaná v kanonickom rozložení. .

Zapíšme si maticu systému a pomocou ďalších elementárnych transformácií ju prenesme do postupného zobrazenia: