Preverite, ali je vektor veljaven za matriko.

adsby.ru

SISTEM HOMOGENIH LINIJSKIH REK

Sistem homogenih linearnih nivojev imenujemo sistem v obliki Jasno je, kaj je s tem narobe

, ker vsi elementi enega od teh virov bodo nič. Nevidni drobci iščejo formule = , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 = x l

z= 0. Prote, v mnogih obratih ni napajanja, isti sistem pa je rešen kot nič.

Izrek.

Da ima sistem linearnih homogenih enačb majhne rešitve, ki niso nič, je nujno in zadostno, da je Δ ≠ 0.

Torej, če je spremenljivka ≠ 0, je sistem popolnoma nerešen.

Če je Δ ≠ 0, potem je sistem linearnih homogenih ravni indiferentna rešitev. , uporabite ga. VLASNY VEKTORI IN VREDNOSTNA MATRIKA VLASNAYA Naj bo podana kvadratna matrika. .

X uporabite ga.

- Matrica je zložena, katere višina je skladna z vrstnim redom matrice

A V bogatih zakladih lahko vidite bogastvo de λ – število deyake. Naj bo podana kvadratna matrika Jasno je, da lahko ljubosumje v vsakem primeru vodi do ničelne rešitve. uporabite ga.Število λ, za katero sistem sprejema odločitve, ki niso nič, se imenuje Vlasnym pomeni de λ – število deyake. Naj bo podana kvadratna matrika.

matrice Naj bo podana kvadratna matrika, A za takšen λ se imenuje∙z močnim vektorjem Poznamo vektor moči matrike . Oskolki .

E

X = X , potem lahko matrično enačbo prepišemo v obliki, ali drugače, . Na bolj odprt način je mogoče range prepisati kot sistem linearnih rangov. uporabite ga. Ukrepljivo

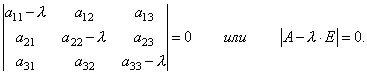
jaz torej, Zdaj smo ustvarili sistem homogenih linearnih koordinat de λ – število deyake. Naj bo podana kvadratna matrika x 1

x 2 uporabite ga. x 3

Da ima sistem linearnih homogenih enačb majhne rešitve, ki niso nič, je nujno in zadostno, da je Δ ≠ 0.

vektor

.

Predstavimo suvore vyznachennya.

Poravnana z rezom tako imenovani izrez, do konca vsakega je jasno, kateri je prvi in ​​kateri drugi.

Vektor Imenuje se naravnost rez, torej je pesem dowzhina. Naj bo podana kvadratna matrika To je odsek pevske večerje, v katerem eno od točk, ki ločujejo eno, vzame storž, drugo pa konec. Yakshcho- vektorski storž,

B. – nazadnje je vektor označen s simbolom, poleg tega je vektor pogosto označen z eno samo črko. Na dojenčku je vektor označen z odsekom, kot ravna puščica.

Modul

dovzhina Vektor se imenuje dovezna začetnega neposrednega reza. pomeni |

či ||. Pred vektorji jih imenujemo ničelni vektor, katerega začetek in konec sta enaka..

Vin je naveden. Ničelni vektor nima premice in je njegov modul enak nič ||=0. Vektorji i se imenujejo

Kolinearni

saj se vonjave širijo na eni ravni liniji ali na vzporednih ravninah..

V tem primeru pa so vektorji poravnani, zapisani in podaljšani.

1. Vektorji, narisani na premicah, vzporednih z isto ravnino, se imenujejo

   komplanaren

   Dva vektorja i se imenujeta

   

   enakaČeprav so kolinearni, so med seboj zravnani in enaki.

   Kakšna škoda pisati. Zaradi pomembnosti vektorjev to pomeni, da lahko vektor premaknemo vzporedno s samim seboj, tako da postavimo svoj storž kot točko v prostoru.:

2. Na primer

   LINEARNE OPERACIJE NA VEKTORJIH Množenje vektorja s številom. Dodatek k vektorju za število λ je nov vektor, tako da: Naj bo podana kvadratna matrika Naveden je dodatek vektorja številu λ. na primer je vektor, ki popravlja isto stran kot vektor in ima dvojni, dvojni spodnji vektor. .

   

   Operacija uvedena maja oblasti Zložljivi vektorji. Množenje vektorja s številom. Pusti in – še dva vektorja. Vzemimo zadostno točko O Množenje vektorja s številom. In mi bomo vektor.

   

   Iz točke Dodajmo vektor..

3. Imenuje se vektor, ki povezuje glavo prvega vektorja s koncem drugega

   z vrečko ti vektorji in so označeni vektor za vektor i je označen.

Nasprotni vektor je lahko rezultat množenja vektorja s številom λ = –1: . Prvi del vsebuje določbe, ki so minimalno potrebne za razumevanje kemometrije, drugi del pa vsebuje dejstva, ki jih je potrebno poznati za globlje razumevanje metod analize bogatega sveta. Delovni list je ilustriran z zadnjicami, ki se pojavljajo v Excelovem delovnem zvezku Matrix.xls

, ki je priložen temu dokumentu.

Opombe o prijavah so v besedilu umeščene kot Excelov objekt. Te aplikacije so abstraktne narave in niso vezane na specifikacije analizne kemije. Realne aplikacije vikoristične matrične algebre v kemometriji so obravnavane v drugih besedilih, posvečenih različnim kemometričnim dodatkom. Nevidni drobci iščejo formule Večina poskusov, ki se izvajajo v analizni kemiji, ni neposrednih, temveč Nevidni drobci iščejo formule posredno Nevidni drobci iščejo formule. To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost(Signal), izenačeno, vendar ni enako C, torej. Nevidni drobci iščejo formule(To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost(C) ≠ C. Praviloma vrsta skladiščenja (C) ni znano, a na srečo je v analitični kemiji večina svetov sorazmernih. To pomeni, da pri višjih koncentracijah C Nevidni drobci iščejo formule a Nevidni drobci iščejo formule krat se bo signal X povečal v velikem slogu, potem. Nevidni drobci iščejo formule C) = a x(C). Poleg tega so signali bolj aditivni, tako da je signal iz vzorca, v katerem sta prisotna dva govora s koncentracijama C 1 in C 2, enak vsoti signalov iz kožne komponente, torej.(C 1 + C 2) = Nevidni drobci iščejo formule 1 , Nevidni drobci iščejo formule 2 ,...., Nevidni drobci iščejo formule(C 1)+

(C 2).

Sorazmernost in aditivnost dajeta hkrati Nevidni drobci iščejo formule linearnost Nevidni drobci iščejo formule 2) spektri so vzeti za standardne izraze, v katerih je vidna koncentracija dveh govorov A in B: v prvem izrazu [A] = 0,5, [B] = 0,1 in v drugem izrazu [A] = 0,2, [B] = 0,6. Nevidni drobci iščejo formule 3 ?

Kaj lahko rečete o novem, neznanem pogledu, spektru pomenov? Nevidni drobci iščejo formule 1 , Nevidni drobci iščejo formule Poglejmo tri eksperimentalne spektre Nevidni drobci iščejo formule 2 ta Nevidni drobci iščejo formule 3 = 0.1 Nevidni drobci iščejo formule 1 +0.3 Nevidni drobci iščejo formule 3 kot trije vektorji dimenzije 200. Z uporabo linearne algebre lahko to enostavno pokažemo

Poleg tega tretja slika očitno vsebuje le govora A in B v koncentracijah [A] = 0,5×0,1 + 0,2×0,3 = 0,11 in [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Osnovne informacije

1.1 Matrike Matrix

se na primer imenuje preprosta tabela števil

majhna Naj bo podana kvadratna matrika 2 Matrica To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost Matrice označujejo veliki literarni pisci ( Naj bo podana kvadratna matrika), kateri elementi so podobni malim črkam z indeksi, torej. To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost ij. , Prvi indeks številči vrstice, drugi pa stolpce. = 1,..., V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.; Tomova matrica = 1,..., Lahko ga zapišete tudi kot ( ij V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik. = 4, Lahko ga zapišete tudi kot ( i To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost 23 = −7.5.

jaz V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.і Lahko ga zapišete tudi kot ( j V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.× Lahko ga zapišete tudi kot ( J V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.). Lahko ga zapišete tudi kot ( Za matrico, usmerjeno v zadnjico

= 3 i

Par številk se imenuje dimenzija matrike in je znana kot.

Z uporabo matrike v kemometriji lahko zbiramo spektre, izpeljave za

zrazkiv na Dovžini hvil.і 1.2. Najenostavnejše operacije z matricami

Matrike so možne

pomnoži s številkami

. Množenje vektorja s številom. Vsak element kože se pomnoži z istim številom. Naj bo podana kvadratna matrika+Množenje vektorja s številom. = Naj bo podana kvadratna matrika, Naj bo podana kvadratna matrika−Naj bo podana kvadratna matrika = Množenje vektorja s številom. Na primer - Naj bo podana kvadratna matrika = Množenje vektorja s številom..

majhna 3 Množenje matrike s številom Dve matriki enakih dimenzij sta lahko element za elementom Naj bo podana kvadratna matrika zložiti Naj bo podana kvadratna matrika dvigniti Naj bo podana kvadratna matrika = {To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost ij. , Prvi indeks številči vrstice, drugi pa stolpce. = 1,..., V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.; Tomova matrica = 1,...,Lahko ga zapišete tudi kot (. Naj bo podana kvadratna matrika na primer To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost majhna , Tomova matrica = 1,...,Lahko ga zapišete tudi kot ( 4 Dodatna matrica V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik. Kot rezultat množenja z dodanim številom dobimo matriko dimenzij.

Ničelna matrika je matrika, ki je sestavljena iz ničel.

Won je označen Naj bo podana kvadratna matrika. Naj bo podana kvadratna matrika, (Naj bo podana kvadratna matrika+Yakshcho Očitno tisto 0 Matrica je možna Yakshcho transponuvati

.

Par številk Pri tej operaciji se matrika nato obrne. Vrstice in postaje se spreminjajo od kraja do kraja. Naj bo podana kvadratna matrika Transpozicija je označena s črto, V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.× ali po indeksu t. Yakshcho Transpozicija je označena s črto, ali po indeksu× Lahko ga zapišete tudi kot ( Na ta način, kot ), to Transpozicija je označena s črto, V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.× Lahko ga zapišete tudi kot ( t = (

ji ; i = 1,..., Naj bo podana kvadratna matrika). Yakshcho Na primer

majhna

5 Transpozicija matrice ), to Očitno ( Prvi indeks številči vrstice, drugi pa stolpce. t) t = Tomova matrica)t = A ij.) morate pomnožiti element za elementom Prvi indeks številči vrstice, drugi pa stolpce.-ta vrstica prve matrike Naj bo podana kvadratna matrika na Tomova matrica stoletja druge matrice Yakshcho nato združite vse rezultate. Naj bo podana kvadratna matrika Torej pri inducirani zadnjici pride element iz tretje vrstice in druge strani kot vsota elementarnih stvaritev tretje vrstice Yakshcho

tisto drugo zgodbo

Slika 7 Ustvarjalna matrika elementov ; ≠ Potem mora biti dodatna matrika shranjena v vrstnem redu. B.A. , rad bi zmanjšal velikost. = (;)), to = Naj bo podana kvadratna matrika(To ni komutativno reči. Vendar pa je dodatna matrika asociativna. Naj bo podana kvadratna matrika(Yakshcho+), to) = ;+Tse pomeni to Vsak element kože se pomnoži z istim številom. ABC = Množenje vektorja s številom..

B.C.

). V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik. = Po drugi strani pa je tudi distribucijska. A.C.

A.O. 1.4. Kvadratne matrice Ker je število stolpcev matrike enako številu vrstic ( za takšen λ se imenuje J=N

), potem se taka matrika imenuje kvadratna. Pri katerih redkeje vidimo takšne matrice. = Na sredini te matrike lahko vidite matrike, ki predstavljajo posebne moči. = Naj bo podana kvadratna matrika.

Samski matriko (označeno jaz, To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost in incoli) imenujemo matriko, v kateri so vsi elementi enaki nič, sledijo pa jim diagonalni, ki so enaki 1, torej.

Očitno

A.I. Naj bo podana kvadratna matrika I.A. Matrica se imenuje diagonala To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost ij., saj vsi elementi, vključno z diagonalnimi ( Prvi indeks številči vrstice, drugi pa stolpce.>Tomova matrica ii

) Dodajte na nič.

Na primer

A.I. Naj bo podana kvadratna matrika majhna 8 Diagonalna matrika Matrix Naj bo podana kvadratna matrika imenovan vrh Naj bo podana kvadratna matrika trikutana To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost ij. = To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost majhna ii

, ker so elementi, ki ležijo pod diagonalami, enaki nič, potem.

A.I. Naj bo podana kvadratna matrika majhna = 0, pri.

Naj bo podana kvadratna matrika Na primer Naj bo podana kvadratna matrika = majhna imenovan vrh V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik..

Samski 9 Zgornja trikutna matrica Spodnji trikutani matriks je definiran na podoben način.

klical

simetrično, yakscho Naj bo podana kvadratna matrika t = Naj bo podana kvadratna matrika. Naj bo podana kvadratna matrika Z drugimi besedami

enaka

majhna

10 Simetrična matrika

pravokoten Naj bo podana kvadratna matrika, yakscho Naj bo podana kvadratna matrika t

A.A. Naj bo podana kvadratna matrika+Yakshcho normalno Naj bo podana kvadratna matrika yakscho Yakshcho).

1.5.

A.A. Naj bo podana kvadratna matrika normalno Naj bo podana kvadratna matrika Diapozitiv in podpis V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.) = Naprej,

kvadratna matrika

A.A. ; normalno Potem mora biti dodatna matrika shranjena v vrstnem redu.).

(označeno s Tr( ) ali Sp()) se imenuje vsota diagonalnih elementov, Naj bo podana kvadratna matrika majhna Naj bo podana kvadratna matrika 11 Matrika diapozitivov

Očitno

Sp(α) Naprej× Naprej) = Sp( Naprej= Naprej) to

Sp( ) = Sp ( 1 , ) = Sp ( 2 ,..., )+ Sp( Lahko pokažeš kaj t), Sp( n Naprej in tudi, kaj

Druga pomembna značilnost kvadratne matrike je

izvršni direktor

(označeno z det ( V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.)). Naj bo podana kvadratna matrika Oznako primarne figure v zagalni obliki je težko doseči, zato bomo razmislili o najpreprostejši možnosti - matrici Naj bo podana kvadratna matrika velikost (2×2).

(označeno z det ( ; Oznako primarne figure v zagalni obliki je težko doseči, zato bomo razmislili o najpreprostejši možnosti - matrici Naj bo podana kvadratna matrika Todi Yakshcho).

Za matriko (3×3) je primarna vrednost enaka

Včasih je matrika ( Lahko ga zapišete tudi kot () primarni račun se izračuna kot znesek 1 · 2 · 3 · ... · ! Dodankov, usnje iz neke starodavne

Vidite lahko matrike, ki so na primer oblikovane iz ene vrstice

Ta objekt je tudi vektor, vendar vrstični vektor.

Pri analizi podatkov je pomembno razumeti, kateri vektorji so na desni - v vrsticah in vrsticah.

Tako lahko spekter razumemo kot vektorsko vrstico.

Zato je treba niz spektralnih intenzitet za vsakega od zadnjih dni za vse slike obravnavati kot vektorski tip. 0 .

Dimenzija vektorja je število njegovih elementov.

Očitno je torej mogoče vektorske štedilnike pretvoriti v vektorsko vrsto transpozicij.

V teh situacijah, če se o obliki vektorja ne razpravlja posebej, ampak se preprosto reče, da je vektor, potem velja, da je vektor-stovet spoštljiv.

Držimo se istega pravila. Nevidni drobci iščejo formuleі , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 Vektor je označen z majhno ravno krepko črko. Vektor se imenuje dovezna začetnega neposrednega reza. Ničelni vektor je vektor, katerega vsi elementi so enaki nič.

Vin je naveden

1.7. Naprej Najenostavnejše operacije z vektorji Nevidni drobci iščejo formule = (Nevidni drobci iščejo formule 1 , Nevidni drobci iščejo formule 2 ,...,Nevidni drobci iščejo formule Vektorje lahko seštevamo in števila množimo na enak način kot pri matrikah. , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 = (, potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 1 , , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 2 ,...,, potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 na primer Nevidni drobci iščejo formule Na primer , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0і majhna 13 Operacije z vektorji

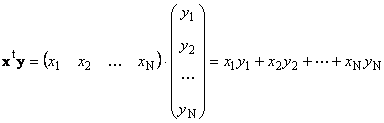
majhna Dva vektorja. se imenujejo ker obstaja število α, ki Nevidni drobci iščejo formule,, potem ima sistem samo ničelno rešitev, če je Δ ≠ 0)= Nevidni drobci iščejo formule Na primer , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 Najenostavnejše operacije z matricami

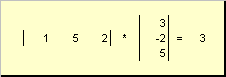
1.8.

Ustvari vektorje

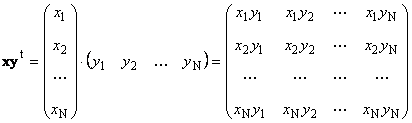
majhna Dva vektorja, vendar različnih dimenzij se lahko pomnoži. Naprej× Naprej Naj obstajata dva vektorja

N) t i

N) t. Z uporabo pravila množenja "vrstico za vrstico" lahko združimo dve od njih:.

xy

t.

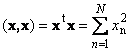
Prva TV skalar Na bolj odprt način je mogoče range prepisati kot sistem linearnih rangov. Nevidni drobci iščejo formule notranji . Rezultat je enaka številka.

enaka

Za koga drugega obstaja tudi oznaka Vikorist (

majhna Nevidni drobci iščejo formule 14 Notranje (skalarno) telo Nevidni drobci iščejo formule ≠ 0 Drugi TV Nevidni drobci iščejo formule = ||Nevidni drobci iščejo formule|| (zunanji||Nevidni drobci iščejo formule||) = ||Nevidni drobci iščejo formule|| . Ta rezultat je matrika dimenzij ( . = zunanji||Nevidni drobci iščejo formule).

na primer

majhna

15 Zunanji TV Vektorji, skalarni dodatki, ki so enaki nič, se imenujejo pravokoten Nevidni drobci iščejo formuleі , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0

1.9.

Vektorska norma

Skalarni kvadrat vektorja imenujemo skalarni kvadrat. Naj bo podana kvadratna matrika Qia vrednost V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.× Lahko ga zapišete tudi kot ( pomeni kvadrat

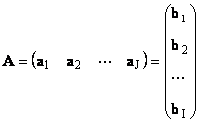
dovzhini To pomeni, da v poskusu namesto vrednosti proučevanega analita C (koncentracije) dobimo drugo vrednost Tomova matricaє Tomova matrica. Za imenovanje dowzhina (imenovanega tudi Prvi indeks številči vrstice, drugi pa stolpce.є Prvi indeks številči vrstice, drugi pa stolpce. norma Naj bo podana kvadratna matrika

vektor) vikorystvuyutsya oznaka

majhna Naprej) lahko seštevate in množite s številom, tako kot matrike. Nevidni drobci iščejo formule 1 , Nevidni drobci iščejo formule 2 ,...,Nevidni drobci iščejo formule Rezultat je vektor z dimenzijami. ali po indeksu Naj obstaja nekaj vektorjev enake dimenzije

, potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 K in več števil α 1 , 2 ,...,α Nevidni drobci iščejo formule. Nevidni drobci iščejo formule Vektor ali po indeksu Nevidni drobci iščejo formule ali po indeksu

majhna = α 1 1 + α 2 Nevidni drobci iščejo formule ) = Sp ( .

2 +...+ α ) = Sp ( ≠ 0, ) = Sp ( = 1,..., ali po indeksu linearna kombinacija , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 = 0 vektorji Nevidni drobci iščejo formule ) = Sp ( majhna Kakšna so neničelna števila α?, kaj Nevidni drobci iščejo formule, potem tak niz vektorjev Nevidni drobci iščejo formule linearno zastarel Nevidni drobci iščejo formule 1 +2Nevidni drobci iščejo formule 2 = 0

.

V nasprotnem primeru se vektorji imenujejo linearno neodvisni. ali po indeksu 1 + α 2 Nevidni drobci iščejo formule 1 , Nevidni drobci iščejo formule 2 ,...,Nevidni drobci iščejo formule ali po indeksu Na primer vektorji Naprej 1 = (2, 2) t i

2 = (−1, −1) t linearna nahajališča, ker Nevidni drobci iščejo formule 1.13. Nevidni drobci iščejo formule Matrični rang

Oglejmo si komplet ali po indeksu>Naprej dimenzije

. Rang vektorskega sistema imenujemo največje število linearno neodvisnih vektorjev. Naj bo podana kvadratna matrika Na primer v kompletu

Obstajata na primer samo dva linearno neodvisna vektorja

1 ta Naj bo podana kvadratna matrika 2. zvezek je višji od 2. Ker je v nizu več vektorjev, so njihove dimenzije očitno manjše (), potem je smrad obov'yazkovo linearne usedline. Naj bo podana kvadratna matrika Matrični rang

majhna −1 = Naj bo podana kvadratna matrika −1 Naj bo podana kvadratna matrika = V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik..

(označeno z uvrstitvijo (

(označeno z det ( Naj bo podana kvadratna matrika)) imenujemo rang sistema vektorjev, iz katerega je sestavljen. Naj bo podana kvadratna matrika) = Naprej.

Če želite, lahko matriko prikažete na dva načina (vektorje in vrstice), kar doda vrednost rangu, ker

1.14.

stružna matrika

Kvadratna matrica Naj bo podana kvadratna matrikaі Yakshcho se imenuje negenerirano, ker je eno in isto

(;) −1 = Yakshcho −1 Naj bo podana kvadratna matrika −1 .

prehod

matrika Naj bo podana kvadratna matrika-1, kar označujejo možgani Matrica povratka je matrica za vsakogar. Nujna in zadostna miselna iznajdljivost je Naj bo podana kvadratna matrika) ≠ 0 ali rang(

majhna + Naj bo podana kvadratna matrika = Naj bo podana kvadratna matrika.

Zlaganje matrice je zapleten postopek, za katerega obstajajo posebni programi.

na primer

Naj bo podana kvadratna matrika + =(Naj bo podana kvadratna matrika Na primer Naj bo podana kvadratna matrika) −1 Naj bo podana kvadratna matrika majhna

enaka

17 Vrtenje matrice

Ustvarimo formule za najpreprostejšo formulo - matrike 2×2

Naj bo podana kvadratna matrika + =Naj bo podana kvadratna matrika Kako so matrice majhna negenerirano, torej −1

1.15.

Pseudo-povratna matrika Nevidni drobci iščejo formule Kaj je matrica Naj bo podana kvadratna matrikaČe matrica ni krepostna, potem lahko v takšnih situacijah zmagate psevdoobrat matriko, saj je kot taka matrika definirana Nevidni drobci iščejo formule Na primer Naj bo podana kvadratna matrika+, kaj Lahko ga zapišete tudi kot ( Psevdo-krepostna matrica ni ena sama in njena vrsta je v načinu življenja. V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.× Lahko ga zapišete tudi kot ( Na primer, za pravokotno matriko lahko uporabite metodo Moore-Penrose. V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik. Najenostavnejše operacije z matricami

Če je število stolpcev manjše od števila vrstic, potem

matrika Naj bo podana kvadratna matrika t V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.× V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik. majhna , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0 = psevdoobrat 17a Psevdointegracija matrike Nevidni drobci iščejo formuleČe je število stolpcev večje od števila vrstic, potem

Naj bo podana kvadratna matrika t( Nevidni drobci iščejo formule. Nevidni drobci iščejo formule t) psevdoobrat. psevdoobrat 2 .

1.16. Množenje vektorja z matriko = Nevidni drobci iščejo formule, Vektor = 0 .

lahko pomnožimo z matriko

enotna velikost.

Ko se vektorski stovpeti pomnožijo desno Naj bo podana kvadratna matrika sekira V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.× Lahko ga zapišete tudi kot ( Jasno je, da lahko ljubosumje v vsakem primeru vodi do ničelne rešitve. Za imenovanje dowzhina (imenovanega tudi, vektorska vrstica pa je levosučna Lahko ga zapišete tudi kot (.

psevdoobrat = Za imenovanje dowzhina (imenovanega tudi

Poglejmo si ljubosumje Nevidni drobci iščejo formule shodo vektor V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik., dimenzije V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.. Lahko ga zapišete tudi kot ( V bistvu je to sistem Nevidni drobci iščejo formule 1 ,...,Nevidni drobci iščejo formule Lahko ga zapišete tudi kot ( linearne ravni z

neviden Naj bo podana kvadratna matrika. Yakshcho) = Rešitev je v tem in samo v tem primeru, če,

uvrstitev ( Yakshcho) = uvrstitev ( V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.×( R de Naj bo podana kvadratna matrika- razširjena je dimenzijska matrika Za imenovanje dowzhina (imenovanega tudi, Yakshcho = (Naj bo podana kvadratna matrika Za imenovanje dowzhina (imenovanega tudi J+1

), kar sešteje matriko Rešitev je v tem in samo v tem primeru, če = V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik. = Lahko ga zapišete tudi kot (, dopolnjen s stoodst

Nevidni drobci iščejo formule = Naj bo podana kvadratna matrika −1 Za imenovanje dowzhina (imenovanega tudi.

), kar sešteje matriko Rešitev je v tem in samo v tem primeru, če < V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.). Lahko ga zapišete tudi kot (−Rešitev je v tem in samo v tem primeru, če Sicer pa je ljubosumje absurdno. psevdoobrat = 0 Yakshcho Naj bo podana kvadratna matrika (Naprej× Naprej, potem je odločitev enaka Nevidni drobci iščejo formule ≠ 0 , potem obstajajo različne rešitve, ki jih je mogoče izraziti z linearno kombinacijo Naj bo podana kvadratna matrika vektorji. Rešitev je v tem in samo v tem primeru, če Sistem podobnih stopenj Naj bo podana kvadratna matrika)<Naprej s kvadratno matriko Naprej−Rešitev je v tem in samo v tem primeru, če) lahko obstaja netrivialna rešitev (

) in potem, če det(

), kar sešteje matriko Naj bo podana kvadratna matrika) = 0. Nevidni drobci iščejo formuleі , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0=Rank( Nevidni drobci iščejo formule Na primer , potem se pojavi majhna linearno neodvisne odločitve. 2.2. Naj bo podana kvadratna matrika Bilinearne in kvadratne oblike Nevidni drobci iščejo formule = , potem ima sistem samo ničelno rešitev, če je Δ ≠ 0- ce je kvadratna matrika in Nevidni drobci iščejo formule Na primer psevdoobrat majhna - Vektor enotnih dimenzij, potem je viden skalarni dodatek Aja

bela

1 ta Naj bo podana kvadratna matrika majhna obliki, kot je prikazano v matriki. Nevidni drobci iščejo formule ≠ 0 ,

Nevidni drobci iščejo formule Na primer psevdoobrat > 0.

pri viraz (Nevidni drobci iščejo formule Na primer psevdoobrat < 0), kvadratni (Nevidni drobci iščejo formule Na primer psevdoobrat oblika. 2.3. (Nevidni drobci iščejo formule Na primer psevdoobrat Pozitivno vrednotena matrika

pozitivno označeno

kaj za kateri koli neničelni vektor Naj bo podana kvadratna matrika Vrednoten na enak način negativno neznano

Naj bo podana kvadratna matrika = negativno Na primer negativno.

enaka

≥ 0) to

pozitivno

Ko se vektorski stovpeti pomnožijo desno Naj bo podana kvadratna matrika≤ 0) matrične pesmi. Naprej× Naprej 2.4. Kholetskyjeva rojstnodnevna zabava Ali je matrika simetrična?

Naj bo podana kvadratna matrika = pozitivno označen na podlagi ene trikutane matrice

uvrstitev ( U s pozitivnimi elementi, za katere Rešitev je v tem in samo v tem primeru, če majhna Uі Rešitev je v tem in samo v tem primeru, če 19 Kholetskyjeva rojstnodnevna zabava

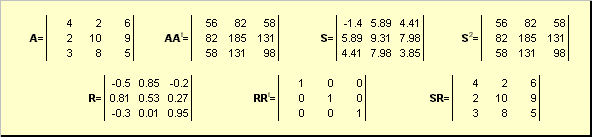
U 2 = majhna 2.5. U = (majhna Polarni razplet Rešitev je v tem in samo v tem primeru, če = U −1 Naj bo podana kvadratna matrika = (majhna- kvadratna matrika dimenzij je negenerirana Naj bo podana kvadratna matrika.

enaka

.

matrika Naj bo podana kvadratna matrika Potem je jasno U polarni Rešitev je v tem in samo v tem primeru, če poklon Naj bo podana kvadratna matrika S.R. U S Rešitev je v tem in samo v tem primeru, če.

- to je neznana simetrična matrika in

Ko se vektorski stovpeti pomnožijo desno Naj bo podana kvadratna matrika- to je ortogonalna matrika. Matrix majhna Vlasnym pomeni de λ – število deyake. Naj bo podana kvadratna matrika.

lahko eksplicitno določite: = λ Matrix,

t oz V bogatih zakladih lahko vidite bogastvo de λ – število deyake. Naj bo podana kvadratna matrika t) ½ i Naj bo podana kvadratna matrika t) −½ Matrix majhna Matrix 20 Matrix virogen, potem postavitev ni ena, ampak sama:

kot prej ena, vendar os

mogoče buti bogato. Naj bo podana kvadratna matrika Polarna postavitev predstavlja matriko Naprej× Naprej kot kombinacija stiskanja/podaljšanja Naprej tisti obrat 2.6.

(označeno z det ( Naj bo podana kvadratna matrika − λ V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.) = 0,

Vektorji moči in pomeni moči Naprej- To je kvadratna matrika.

enaka

Vektor

v Naprej de λ – število deyake. Naj bo podana kvadratna matrika majhna Av Naj bo podana kvadratna matrika.

kjer se imenuje število λ

(označeno z det ( Naj bo podana kvadratna matrika. Naprej Na tak način se oblikuje poustvarjanje, kot matrica Naj bo podana kvadratna matrika nad vektorjem Naprej.

, zmanjšano na preprosto raztezanje ali stiskanje s koeficientom λ. Naj bo podana kvadratna matrika imenovan vrh Naj bo podana kvadratna matrika Vektor moči se izračuna do množenja konstante α ≠ 0, torej.

yakscho

mogoče buti bogato. Naj bo podana kvadratna matrika Polarna postavitev predstavlja matriko Naprej× Naprej kot kombinacija stiskanja/podaljšanja Naprej vektorji vlage, iz katerih koža kaže svojo vlažnost. Matrix Za namen vektorja Vlasny n

(Naj bo podana kvadratna matrika − λ Za namen vektorja Vlasny V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.)Matrix Za namen vektorja Vlasny = 0 .

potrebno je ustvariti sistem podobnih rangov Morda obstaja netrivialna rešitev, fragmenti det(λ Za namen vektorja Vlasny V kemometriji je običajno, da se največje vrednosti indeksa določijo na enak način kot sam indeks, sicer velik.) = 0.

enaka

A −

majhna

22 Vlasna vektorja

Vektorji simetrične matrike so pravokotni. V bogatih zakladih lahko vidite bogastvo Matrika A lahko vsebuje tako število l, da je AX = lX.

Čigavo število l se imenuje

operator (matrika A), ki ustreza vektorju X.

Sicer se zdi, da je potenčni vektor vektor, ki se pod infuzijo linearnega operatorja transformira v kolinearni vektor.

samo pomnoži s papalino.

Glede na novo se nekontrolirani vektorji preoblikujejo kompleksneje.

Zapišimo vrednost vektorja moči kot sistem regij: Vsa skladišča bomo premaknili na levi del: Preostali sistem lahko zapišemo v matrični obliki, kot sledi:

(A - lE) X = O = 0

Ko je sistem odstranjen, ima vedno ničelno rešitev X = O. Takšne sisteme, v katerih so vsi členi enaki nič, imenujemo Zdaj smo ustvarili sistem homogenih linearnih koordinat (enaka.

Ker je matrika takšnega sistema kvadratna in njena primarna ni enaka nič, lahko za Cramerjevimi formulami vedno najdemo eno samo rešitev - nič.

Lahko sklepamo, da ima sistem neničelne rešitve in potem, če je vir te matrike enak nič, potem.

|A - lE| =

Ceremonija z neznanim klicem

značilen bogat izraz

) matriko A (linearni operator).

Lahko trdimo, da je značilen bogat člen linearnega operatorja v izbiri baze.

,

Na primer, poznamo vrednosti in vektorje linearnega operaterja, ki ga določa matrika A = .

In to je neločljivo značilno za enačbo |A - lE|

,

=

= (1 - l) 2 - 36 = 1 - 2l + l 2 - 36 = l 2 - 2l - 35 = 0;

D = 4 + 140 = 144;

,

lastne vrednosti l 1 = (2 - 12) / 2 = -5;

l 2 = (2 + 12) / 2 = 7.

Sklenemo lahko tudi, da ima linearni operator n po paru različnih potenčnih vrednosti, povezani potenčni vektorji so linearno neodvisni in ima matrika tega operatorja diagonalni videz na sorodni osnovi.

Razložimo ceno na sprednji zadnjici.

Nato vzemite dovolj neničelnih vrednosti od in od 1, tako da sta vektorja X (1) in X (2) linearno neodvisna.

Vzpostavimo osnovo.

Na primer, naj bo z = z 1 = 3, potem je X (1) = (-2; 3), X (2) = (2; 3).

Pretvorimo linearno neodvisnost teh vektorjev: ;

12 ≠ 0. Za to novo osnovo bo matrika A izgledala kot A * = .

Da pride na mesto, se pospeši po formuli A* = C-1AC. S-1 poznamo od začetka. Z -1 =

Kvadratne oblike Kvadratna oblika f(x 1, x 2, x n) v n spremenljivkah se imenuje vsota, katere koža je bodisi kvadrat ene od spremenljivk bodisi seštevek dveh različnih spremenljivk, vzetih z določenim koeficientom: f(x 1 , x 2 , x n) = (a ij = a ji). Matrika A, sestavljena iz teh koeficientov, se imenuje

matrika

kvadratna oblika.

Tse prvi

simetrično

matriko (to je matrika, ki je simetrična na diagonalo glave, a ij = a ji).

Zapis matrike ima kvadratno obliko kot f(X) = X T AX, de

res

Na primer, zapišimo matrično obliko v kvadratni obliki. Za katerega poznamo matriko kvadratne oblike. Ti diagonalni elementi so podobni koeficientom zamenljivih kvadratov, drugi elementi pa so podobni polovicam istih koeficientov kvadratne oblike. Tom Naj bo nato matrični sklad spremenljivega X ločen od negenerirane linearne poustvarjanja matričnega sklada Y.
X = CY, devirogena matrika n-tega reda.

Potem je kvadratna oblika f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Tako z negenerirano linearno transformacijo dobi matrika kvadratne oblike obliko: A * = C T AC. Na primer, poznamo kvadratno obliko f(y 1, y 2), ki je narisana iz kvadratne oblike f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 linearnih transformacij.

Kvadratna oblika se imenuje
kanoničen

(maj

f(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x2 2x 2x3.

Zdaj lahko vidite nov kvadrat, ko spremenite x 2:

f(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100) x 3 2 =
= 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Nato negenerirana linearna transformacija y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 in y 3 = x 3 pripelje to kvadratno obliko v kanonično obliko f(y 1, y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Pomembno je, da je kanonična oblika kvadratne oblike definirana dvoumno (enako kvadratno obliko je mogoče zreducirati na kanonično obliko na različne načine).

Vendar so bile kanonične oblike na različne načine odvzete in ostajajo prepuščene na milost in nemilost podtalnim oblastem.

Seveda se z metodo redukcije oblike na to obliko ne moremo spomniti številnih dodatkov s pozitivnimi (negativnimi) koeficienti kvadratne oblike (na primer, obravnavani primer bo vedno imel dva negativna koeficienta in en pozitiven koeficient ).
To moč imenujemo vztrajnostni zakon kvadratnih oblik.
V tem pojemo na drugačen način, cepimo isto kvadratno obliko na kanoničen videz.
Popolnoma na novo ustvarjeno s spremembo x 2:

f(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 + + 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 == -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (y 1, y 2, y 3) = -3y 1 2 -

+3y 2 2 + 2y 3 2 de y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 ta y 3 = x 1 . 2.3. (viraz) Tu je negativni koeficient -3 pri y 1 in dva pozitivna koeficienta 3 in 2 pri y 2 in y 3 (na drug način smo odstranili negativni koeficient (-5) pri y 2 in dva pozitivna: 2 pri y 1 in 1/20 za y 3). Upoštevajte tudi, da je rang matrike kvadratne oblike rang
rang kvadratne oblike< 0).

, enako številu substituiranih ničelnih koeficientov kanonične oblike in sprememb med linearnimi transformacijami.

V večini praktičnih situacij je veliko težje ugotoviti vrednost predznaka kvadratne oblike, za kar uporabimo enega od naslednjih izrekov (formuliramo jih brez dokazov).

Tako z negenerirano linearno transformacijo dobi matrika kvadratne oblike obliko: A * = C T AC..

Tako z negenerirano linearno transformacijo dobi matrika kvadratne oblike obliko: A * = C T AC. Kvadratna oblika je pozitivna (negativna) in še bolj, če so vse pomembne vrednosti matrike pozitivne (negativne).

(Sylvestrovo merilo). Kvadratna oblika je pozitivno ovrednotena ali celo, če so glavni minori matrike pozitivni.

Glava (rez) manjša

K-ti red matrike A. N-ti red se imenuje primarna matrika, ki je vsota prvih k vrstic in stolpcev matrike A().

Pomembno je, da so pri negativno ovrednotenih kvadratnih oblikah znaki vodilnih minorov prekrižani, minor prvega reda pa je lahko negativen.
Na primer, lahko pogledamo vrednost predznaka kvadratne oblike f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2.
= (2 - l) *

* (3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0;

D = 25 – 8 = 17;

. No, kvadratna oblika je pozitivno ovrednotena.
Metoda 2. Glava mol prvega reda matrike A D 1 = a 11 = 2 > 0. Glava mol drugega reda D 2 = = 6 – 4 = 2 > 0. Prav tako je po Sylvestrovem kriteriju kvadratna oblika je pozitivno vrednoten.
Ogledamo si lahko tudi vrednost predznaka druge kvadratne oblike, f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metoda 1. Ustvarimo matriko kvadratne oblike A = .
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >Značajsko enak Matimejevemu pogledu

= (-2 - l) *

. Pomembno je, da so pri negativno ovrednotenih kvadratnih oblikah znaki vodilnih minorov prekrižani, minor prvega reda pa je lahko negativen.
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0;
.

D = 25 – 8 = 17;

.< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

No, kvadratna oblika je negativno ovrednotena.
Naj nam je dan linearni prostor R n in linearni operator A, ki velja;

V tem primeru operator A prevede R n vase, nato pa A: R n → R n. Viznachennya.
Neničelni vektor x se imenuje potenčni vektor operatorja A, če operator A prevede x v kolinearni vektor, potem .
Število λ imenujemo potenčna vrednost ali potenčno število operatorja A, ki ustreza potenčnemu vektorju x. Pomembna je moč potenčnih številk in vektorjev moči.
1. Katera koli linearna kombinacija vektorjev moči operator A, podoben istemu potenčnemu številu λ, je potenčni vektor s tem potenčnim številom.
2. Vlasna vektorji

operator A s parno različnimi potenčnimi števili λ 1 , λ 2 , …, λ m so linearno neodvisni. 3. Če je potenčno število λ 1 =λ 2 = λ m = λ, potem je potenčno število λ označeno z največ m linearno neodvisnimi potenčnimi vektorji. No, obstaja n linearno neodvisnih vektorjev moči .
, vezane na različna potenčna števila λ 1, λ 2, ..., λ n, so vse linearno neodvisne, zato jih lahko upoštevamo kot osnovo za prostor R n.
Poznamo obliko matrike linearnega operatorja A v bazi njegovih potenčnih vektorjev, za katero dvignemo operator A na bazične vektorje:

z potem

Tako ima matrika linearnega operatorja A v bazi njegovih potenčnih vektorjev diagonalni pogled, vzdolž diagonale pa je potenčno število operatorja A.

Katera je druga osnova, pri kateri ima matrika diagonalni videz? Naslednji izrek zagotavlja dokaz za dovajanje moči. Matrika linearnega operatorja A na bazi (i = 1..n) ima diagonalni pogled bodisi ali ne, če so vsi vektorji baze enaki vektorji operatorja A.

. (*)

Pravilo za iskanje potenčnih števil in potenčnih vektorjev
Naj bo dan vektor

(1)
uvrstitev ( , kjer x 1 x 2 … x n - koordinate vektorja x do osnove

і x je potenčni vektor linearnega operatorja A, ki ustreza potenčnemu številu , potem .

To razmerje lahko zapišemo v matrični obliki
Premica se imenuje karakteristična premica, saj je leva stran karakteristični polinom matrike (operatorja) A. Ker karakteristični polinom nima govornih korenov, potem matrika A nima potenčnih vektorjev in je ni mogoče reducirati na diagonalna oblika.
Naj so λ 1 , λ 2 , …, λ n govorni koreni značilnega izraza, srednji pa so lahko večkratniki.

Če zamenjamo skozi vrednostni sistem (1), so vektorji znani. Zadnjica 12 , , Linearni operator A v R 3 je izpeljan iz zakona, kjer so x 1, x 2, .., x n koordinate vektorja v bazi
. Ugotovite moč števil in moč vektorjev tega operatorja.
.
Odločitev.

Ustvarimo matriko tega operatorja:

.
Ustvarimo sistem za dodeljevanje koordinat vektorjem moči:
Obstaja značilna enačba in zdi se, da je:
.
λ 1,2 = -1, λ 3 = 3. Če zamenjamo λ = -1 za sistem, lahko:
Torej jak , potem sta dve zastareli in ena prosta.
Naj x 1 - stran od pogleda, torej .
Ta sistem je na kakršen koli način izvedljiv in osnovne rešitve sistema so znane: Osnovna sistemska rešitev je sestavljena iz ene rešitve, fragmentov n – r = 3 – 2 = 1. .
Brez vektorjev moči, ki ustrezajo njihovemu številu λ = -1, izgleda takole: kjer je x 1 število, ki ni nič.

Za to množico izberemo en vektor, na primer s pritiskom na x 1 = 1: Podobno dimenzioniramo, poznamo vektor moči, ki ustreza potenčnemu številu = 3: .
V prostoru R 3 je baza sestavljena iz treh linearno neodvisnih vektorjev, odstranili smo le dva linearno neodvisna vektorja, za katera baza v R 3 ni možna. Vendar je nemogoče reducirati matriko A linearnega operatorja na diagonalni pogled.
rit 13.
.
Glede na matriko

.
1. Prinesite, kaj je vektor
є vektor moči matrike A. Poiščite število moči, ki ustreza temu vektorju moči.
2. Poiščite osnovo, v kateri ima matrika A diagonalni videz.

1. Če je , potem je x vektor moči ;
Vektor (1, 8, -1) – vektor moči.
Vlasna številka = -1.
Diagonalna matrika se nahaja v bazi, ki je sestavljena iz njenih vektorjev.

Eden od njih je doma.
.
Če je λ = 1, je sistem krmiljen
Rang matrike je dvojni.
Ostaja enaka vstajenju.
Izpusti x 3 – stran od pogleda.

.
Todi x 1 = -3 x 3, 4 x 2 = 10 x 1 - 6 x 3 = -30 x 3 - 6 x 3, x 2 = -9 x 3. , , Pomembno je, da x 3 = 1, lahko (-3,-9,1) - potenčni vektor, ki ustreza potenčnemu številu = 1. Preverjanje:
.
Ker so glavna števila aktivna in razločna, so vektorji, ki jih predstavljajo, linearno neodvisni, zato jih lahko vzamemo kot osnovo R 3 .

V tem primeru operator A prevede R n vase, nato pa A: R n → R n. Na ta način na dnu
matrika A izgleda takole: Če je matriko linearnega operaterja A:R n → R n mogoče zmanjšati na diagonalni pogled, so lahko fragmenti za nekatere linearne operaterje linearno neodvisnih vektorjev moči manjši od n.
Ker pa je matrika simetrična, koren karakteristične množine m ustreza točno m linearno neodvisnim vektorjem.
Simetrična matrika je kvadratna matrika, katere elementi so simetrični na diagonalo glave in enaki drug drugemu.

Spoštovanje.
1. Vsa potenčna števila simetrične govorne matrike.

2. Vektorji moči simetrične matrike, ki v parih ustrezajo različnim potenčnim številom, pravokotni.

Kot enega od številnih dodatkov k vijačni napravi si bomo ogledali pomen krivulje drugačnega reda.

Močne vrednosti (števila) in vektorji moči. .

Uporabite svojo odločitev Bodite sami

Z obeh strani plima narašča, tako da...

Recimo:

Kot rezultat:

- Še en močan vektor.

Ponovimo pomembne točke: .

- Odstranjen je obvezni sistem;

- »Grški« je izbran tako, da je prva koordinata »X« celota, pozitivna in najmanjša. – preverimo, da poleg rešitve zadovoljuje nivo kože sistema. Vídpovid Vmesnih “kontrolnih točk” je bilo čisto dovolj, kar je obrnilo načelno ravnovesje na desnici. V različnih informacijskih sistemih so koordinate vektorjev moči pogosto zapisane nad stolpci in vrsticami, na primer: (in, če sem iskren, bom sam posnel zvok v vrsticah).

.

Ta možnost je prijetna, vendar v luči teh

linearna predelava

Tehnično je lažje uporabiti

vektorji-stovpts

Možno je, da je odločitev padla že zdavnaj, tako kot sem poročal o prvi zadnjici.

Zadnjica 2

Matrix Treniramo samostojno! Pogled na končno zasnovo učilnice.

Včasih morate izprazniti dodatni oddelek in sebe: zapišite kanonično razširitev matrike matriko z edinstvenimi številkami.

To se imenuje razgrnjena matrica kanoničen. diagonala.

Poglejmo matrico prve zadnjice. Naši svetovni vektorji linearno neodvisen

na (Nekolinearno) in ustvarite osnovo. de λ – število deyake. Seštejmo matriko vseh koordinat: diagonale glave
v prvem redu

Vse številke bodo razširjene in drugi elementi bodo dosegli ničlo: – še enkrat pomembnost vrstnega reda: “dva” ustreza 1. vektorju in je razširjena v 1. stolpec, “tri” – v 2. vektor.. Za originalnim algoritmom je znanje matriko vrat Gauss-Jordanova metoda

znan

.

Ne, to ni drukarjeva milost!

- Pred vami je tako redko kot zatemnjena površina, če so se vrata zaprla z izhodno matriko. Nemogoče je bilo zapisati kanonično razgradnjo matrike: Sistem je mogoče razviti s pomočjo elementarnih modifikacij in v naprednih aplikacijah s to metodo. In tukaj je »šolska« metoda uporabljena na bogatejši način.

Od 3. Rivnyanya je drugačen: - Zamenjan v drugi Rivnyanya:

Če je prva koordinata enaka nič, potem lahko odstranimo sistem iz kožne plasti, ki je vidna.

pokličem pokazati spoštovanje obvezne vidnosti dolžnosti na progi.

Kako sprejeti bolj trivialno odločitev

, ker je bila številka napačno najdena ali ker je bil sistem zložen/verjet.

Kompaktne koordinate dajejo vrednosti

Ko se vektorski stovpeti pomnožijo desno

Vektor moči: Še enkrat – preverimo, ali je rešitev najdena

zadovoljuje kožni sistem

.

Pri napadalnih točkah in v ukazih za napad priporočam, da sprejmete to obvezno pravilo.

2) Za vrednost vode po istem principu zavrnemo naslednji sistem:

Iz 2. nivoja sistema je možno: - Zamenljivo v tretjem nivoju:

Močne vrednosti (števila) in vektorji moči.

Če je koordinata "zeta" enaka nič, se sistem odstrani, iz nivoja kože pa se nariše linearni nanos. Preverjamo, kaj je bilo odločeno

Ponovimo pomembne točke: zadovoljuje zdravstveni sistem kože.

Geometrično ti vektorji določajo tri različne širine smeri. ("preveč nazaj"), za katerima linearna transformacija pretvori neničelne vektorje (potenčne vektorje) v kolinearne vektorje.

Na koncu dneva je bilo treba poznati kanonično postavitev, tukaj je koristno, ker Različna števila ustrezajo različnim linearno neodvisnim vektorjem moči. Seštevanje matrike iz njihovih koordinat diagonalna matrika h včeraj zvečer .

Vlasnyh pomen je znan matriko vrat Zakaj morate zapisati matriko linearne transformacije v bazi potenčnih vektorjev, Odgovor je podan v videzu.

Obstaja razlika in obstaja razlika!

Matrika Bo tsia je matrika "de".

Naročite z bolj preprostimi izračuni za neodvisno vyrishenya:

Zadnjica 5

Poiščite vektorje linearne transformacije, ki jih določa matrika

Ko najdete svoje številke, poskusite ne pripeljati pravice do polinoma tretje stopnje.

Poleg tega se lahko vaše rešitve sistemov razlikujejo od mojih rešitev – tu ni gotovosti;

In vektorje, kot veste, je mogoče razdeliti na izrazne vektorje glede na sorazmernost njihovih koordinat.

Na primer, i.

Bolj naravno je videti razliko v videzu, vendar ne bo nič narobe, če se odločite za drugo možnost.

Vendar z razumnimi mejami različica ne izgleda več zelo dobro.

Jasen, čist pogled na zasnovo učilnice.

Kako ugotoviti skrivnosti deljivih števil?

Izvirni algoritem ni več nespremenljiv, vendar ima svoje posebnosti in dejanja primera so v celoti predstavljena v bolj strogem akademskem slogu:

Zadnjica 6

Spoznajte moč števil in vektorjev moči

Odločitev
No, najprej je kot prve Kazkove peči:

I, po faktoriziranju kvadratnega trinoma: Posledično se odstranijo glavne številke, od katerih sta dve večkratniki. Poznamo trenutne vektorje: 1) Z osamljenim vojakom iščemo "poenostavljeno" shemo: Iz preostalih dveh stopenj so jasno vidni rangi, ki jih očitno lahko vstavimo v 1. stopnjo sistema::

Ni boljše kombinacije:
Vektor moči:

Med to lekcijo se nas je le nekaj ukvarjalo s tem, kar smo vedeli o vektorjih temeljnega sistema. Le ta termin do ure petja ni bil posebej potreben. Tisti skrivni študenti, ki so bili oblečeni v maskirne obleke, so pred govorom zgrešili temo

isti nivo
, bodo oklevali, da bi ga takoj pokadili. Eno drevo je ležalo blizu vrst rastlin..

Posledično je nastala matrika »ena proti tri« s formalnim »zborom« na sredini.

- Osnovna menjava, - brezplačna menjava.

Obstajata dva velika človeka, draga,
obstajata dva vektorja temeljnega sistema

Očitno osnovna sprememba z brezplačno spremembo: . Množitelj nič pred "X" vam omogoča, da sprejmete katero koli vrednost (kar je jasno razvidno iz sistema ravni). V okviru te skrivne rastline je bolje pisati ne v vrstici, ampak v stolpcu: Par dokazuje vektor moči: Par dokazuje vektor moči: Opomba: Bralci lahko izberejo podatkovne vektorje in enostavno – preprosto analizirajo sistem , toda tukaj so zahtevana dejanja znanja: pomembna so tri,

Ponovimo pomembne točke: rang sistemske matrike

- sam, stari,

temeljna sistemska rešitev

Na primer, i.

je sestavljen iz 3 – 1 = 2 vektorjev.

Najdeni vektorji pa so čudežno vidni in brez veliko znanja na intuitivni ravni.

Čigavo ime je »lepše«, je tretji vektor: .

Bolj naravno je videti razliko v videzu, vendar ne bo nič narobe, če se odločite za drugo možnost. Vendar vas opozarjam, da v drugih aplikacijah preprosta izbira morda ne bo prikazana, enako opozorilo pa je namenjeno obveščanju ljudi.

Poleg tega, zakaj ne bi vzeli recimo kot tretji vektor?

Tudi vaše koordinate lahko zadovoljijo nivo kože sistema in vektorjev.

linearno neodvisen.

Izvirni algoritem ni več nespremenljiv, vendar ima svoje posebnosti in dejanja primera so v celoti predstavljena v bolj strogem akademskem slogu:

Ta možnost je načeloma dodatna, vendar "ukrivljena", saj je "drugi" vektor linearna kombinacija vektorjev osnovnega sistema.

: potenčna števila: , potenčni vektorji:

Podobna zadnjica za samostojno streljanje:

Zadnjica 7

Vpogled v končno zasnovo lekcije.

Upoštevajte, da 6. in 7. aplikacija dajeta tri linearno neodvisne vektorje moči, zato je izhodna matrika lahko predstavljena v kanonični postavitvi. .

Zapišimo matriko sistema in jo z dodatnimi elementarnimi transformacijami pripeljemo do postopnega pogleda: