Все, що потрібно знати про трикутник. Перша ознака рівності трикутників. Друга і третя ознаки рівності трикутників Тригонометричні функції зовнішнього кута

Серед величезної кількості багатокутників, які по суті є замкненою ламаною лінією, що не перетинається, трикутник - це фігура з найменшою кількістю кутів. Іншими словами, це найпростіший багатокутник. Але, незважаючи на всю свою простоту, ця постать таїть у собі багато загадок та цікавих відкриттів, які висвітлюються особливим розділом математики – геометрією. Цю дисципліну у школах починають викладати із сьомого класу, і темі «Трикутник» тут приділяється особлива увага. Діти не тільки дізнаються правила про саму фігуру, а й порівнюють їх, вивчаючи 1, 2 та 3 ознаки рівності трикутників.

Перше знайомство

Один із перших правил, з яким знайомляться школярі, звучить приблизно так: сума величин усіх кутів трикутника дорівнює 180 градусам. Щоб це підтвердити, достатньо за допомогою транспортира виміряти кожну з вершин і скласти всі значення, що вийшли. Виходячи з цього, за двох відомих величин легко визначити третю. Наприклад: У трикутнику один з кутів дорівнює 70 °, а інший - 85 °, яка величина третього кута?

180 - 85 - 70 = 25.

Відповідь: 25 °.

Завдання можуть бути і більш складними, якщо вказано лише одне значення кута, а про другу величину сказано лише, на скільки або скільки разів вона більша або менша.

У трикутнику для визначення тих чи інших його особливостей можуть бути проведені спеціальні лінії, кожна з яких має свою назву:

• висота – перпендикулярна пряма, проведена з вершини до протилежної сторони;
• всі три висоти, проведені одночасно, у центрі фігури перетинаються, утворюючи ортоцентр, який залежно від виду трикутника може бути як усередині, так і зовні;
• медіана - лінія, що з'єднує вершину із серединою протилежної сторони;
• перетин медіан є точкою його тяжкості, що знаходиться всередині фігури;
• бісектриса - лінія, що проходить від вершини до точки перетину з протилежною стороною, точка перетину трьох бісектрис є центром вписаного кола.

Прості істини про трикутники

Трикутники, як, власне, і всі фігури, мають свої особливості та властивості. Як уже говорилося, ця фігура є найпростішим багатокутником, але зі своїми характерними ознаками:

• проти найдовшої сторони завжди лежить кут із більшою величиною, і навпаки;
• проти рівних сторін лежать рівні кути, приклад тому - рівнобедрений трикутник;
• сума внутрішніх кутів завжди дорівнює 180 °, що вже було продемонстровано на прикладі;
• при продовженні однієї сторони трикутника за його межі утворюється зовнішній кут, який завжди дорівнюватиме сумі кутів, з ним не суміжних;
• кожна зі сторін завжди менша від суми двох інших сторін, але більша від їх різниці.

Види трикутників

Наступний етап знайомства полягає у визначенні групи, до якої належить представлений трикутник. Приналежність того чи іншого виду залежить від величин кутів трикутника.

• Рівнобедрений - з двома рівними сторонами, які називають бічними, третя у цьому випадку виступає основою фігури. Кути біля основи такого трикутника однакові, а медіана, проведена з вершини, є бісектрисою та висотою.
• Правильний, або рівносторонній трикутник - це той, у якого всі його сторони рівні.
• Прямокутний: один із його кутів дорівнює 90°. У цьому випадку сторона, що протилежить цьому кутку, називається гіпотенузою, а дві інші - катетами.
• Гострокутний трикутник - всі кути менше 90 °.
• Тупокутний - один із кутів більше 90°.

Рівність та подоба трикутників

У процесі навчання не лише розглядають окремо взяту фігуру, а й порівнюють два трикутники. І ця, здавалося б, проста тема має масу правил і теорем, за якими можна довести що фігури, що розглядаються, - рівні трикутники. Ознаки рівності трикутників мають таке визначення: трикутники рівні, якщо відповідні сторони і кути однакові. За такої рівності, якщо накласти ці дві фігури одна на одну, всі їхні лінії зійдуться. Також фігури можуть бути подібними, зокрема це стосується практично однакових фігур, що відрізняються лише величиною. Для того, щоб зробити такий висновок про представлені трикутники, необхідно дотримання однієї з наступних умов:

• два кути однієї фігури дорівнюють двом кутам іншої;
• дві сторони одного пропорційні двом сторонам другого трикутника, а величини кутів, утворених сторонами, дорівнюють;
• три сторони другої фігури такі самі, як і в першої.

Звичайно, для безперечної рівності, яка не викликає жодного сумніву, необхідно мати однакові значення всіх елементів обох фігур, проте з використанням теорем завдання значно спрощується, і для доказу рівності трикутників допускається наявність лише декількох умов.

Перша ознака рівності трикутників

Завдання на цю тему вирішуються з урахуванням докази теореми, яка звучить так: "Якщо дві сторони трикутника і кут, який вони утворюють, дорівнюють двом сторонам і кутку іншого трикутника, то й фігури теж рівні між собою".

Як же звучить підтвердження теореми про першу ознаку рівності трикутників? Всім відомо, що два відрізки рівні, якщо вони однієї довжини, або кола рівні, якщо мають однаковий радіус. А у випадку з трикутниками є кілька ознак, маючи які, можна припустити, що фігури ідентичні, що дуже зручно використовувати під час вирішення різних геометричних завдань.

Як звучить теорема «Перша ознака рівності трикутників», описано вище, а ось її доказ:

• Припустимо, трикутники АВС і А 1 В 1 З 1 мають однакові сторони АВ і А 1 В 1 і, відповідно, ВС і В 1 З 1 , а кути, які утворюються цими сторонами, мають одну й ту саму величину, тобто рівні. Тоді, наклавши ABC на A А 1 В 1 С 1, отримаємо збіг всіх ліній і вершин. Звідси випливає, що це трикутники абсолютно ідентичні, отже, рівні між собою.

Теорему "Перша ознака рівності трикутників" називають ще "По двох сторонах і кутку". Власне, в цьому і полягає її суть.

Теорема про другу ознаку

Друга ознака рівності доводиться аналогічно, доказ ґрунтується на тому, що при накладенні фігур одна на одну вони повністю збігаються по всіх вершинах і сторонах. А звучить теорема так: "Якщо одна сторона і два кути, в освіті яких вона бере участь, відповідають стороні і двом кутам другого трикутника, то ці фігури ідентичні, тобто рівні".

Третя ознака та доказ

Якщо як 2, і 1 ознака рівності трикутників стосувався як сторін, і кутів фігури, то третій належить лише до сторон. Отже, теорема має таке формулювання: "Якщо всі сторони одного трикутника дорівнюють трьом сторонам другого трикутника, то фігури ідентичні".

Щоб довести цю теорему, потрібно детальніше заглибитися в саме визначення рівності. Власне, що означає вираз «трикутники рівні»? Ідентичність говорить про те, що якщо накласти одну фігуру на іншу, всі їх елементи збігатимуться, це може бути тільки в тому випадку, коли їхні сторони та кути будуть рівними. У той же час кут, що протилежить одній зі сторін, яка така сама, як у іншого трикутника, дорівнюватиме відповідній вершині другої фігури. Слід зазначити, що тут доказ легко перевести на 1 ознака рівності трикутників. Якщо така послідовність не спостерігається, рівність трикутників просто неможлива, за винятком тих випадків, коли фігура є дзеркальним відображенням першої.

Прямокутні трикутники

У будові таких трикутників є вершини з величиною кута 90°. Тому справедливі такі твердження:

• трикутники з прямим кутом рівні, якщо катети одного ідентичні катет другого;
• фігури рівні, якщо рівні їх гіпотенузи та один із катетів;
• такі трикутники рівні, якщо їх катети та гострий кут ідентичні.

Ця ознака відноситься до Докази теореми застосовують додаток фігур один до одного, в результаті якого трикутники складають катетами так, щоб з двох прямих вийшов зі сторонами СА і СА 1 .

Практичне застосування

Найчастіше практично застосовується перша ознака рівності трикутників. Насправді така, здавалося б, проста тема 7 класу з геометрії та планіметрії використовується і для обчислення довжини, наприклад, телефонного кабелю без вимірів місцевості, якою він проходитиме. З допомогою цієї теореми легко зробити необхідні розрахунки визначення довжини острова, що є посеред річки, не перепливаючи нею. Або зміцнити паркан, розташувавши планку в прольоті так, щоб вона ділила його на два рівні трикутники, або ж розрахувати складні елементи роботи в столярній справі, або при розрахунку кроквяної системи даху під час будівництва.

Перша ознака рівності трикутників має широке застосування у реальному «дорослому» житті. Хоча у шкільні роки саме ця тема для багатьох здається нудною та зовсім непотрібною.

Конспект уроку

«Перша ознака рівності трикутників»

(Урок №1, 7 клас, за підручником Атанасяна Л.С.)

Цілі уроку:

Навчальна:

Ввести поняття теореми та докази теореми;

Довести першу ознаку рівності трикутників;

Навчити вирішувати завдання застосування першої ознаки рівності трикутників.

Розвиваюча:

Виробити вміння зіставляти, узагальнювати отримані висновки, оцінювати вплив умов на результат;

Розвивати логічне мислення учнів.

Виховна:

Виробити вміння аналізувати дані, виводити логічні наслідки з даних передумов, вміння робити висновки;

Виробити вміння зосереджувати увагу, зосереджуватися.

Методична мета: випробувати новий підхід до формулювання теореми, з'ясувати, чи вловлять учні момент, коли умови стають достатніми.

Тип уроку: комбінований.

Устаткування: комп'ютер, екран, проектор, презентація, лінійка, трикутник,

кольорові крейди.

Хід уроку

Організаційний момент: (2 хв)

На попередньому уроці ми почали вивчення глави «Трикутники». З'ясували, які дві фігури, зокрема два трикутники, називаються рівними. Сьогодні ми з'ясуємо, чи можна встановити рівність двох фігур, не проводячи фактичного накладання однієї на іншу, а порівнюючи лише деякі елементи цих фігур, зокрема, як порівняти трикутники.

Повторення пройденого матеріалу: ( 6 хв)

Повторимо матеріал минулого уроку.

Теоретичне опитування з питань:

поясніть, яка фігура називається трикутником;

накресліть трикутник і покажіть його сторони вершини та кути;

Що таке периметр трикутника?

які трикутники називаються рівними?

Кожному учню видається конвертик, у якому перебуває 6-7 паперових трикутників; учням пропонується знайти у тому числі рівні.

Коли пошук закінчено, спитати одного з учнів, як він знайшов цю пару. Учень розповість, як він накладав трикутник на інший.

Виконання практичного завдання з наступною усною перевіркою:

№1: На дошці (або слайді) накреслено ∆DEK, ∆MNP.

Малюнок 1

Назвіть кути:

а) ∆DEK, що належать до сторони ЄК;

б) ∆MNP, що належать до сторони MN.

Назвіть кут:

а) ∆DEK, укладений між сторонами DE та DК;

б) ∆MNP, укладений між сторонами NP та РМ.

Між якими сторонами:

а) ∆DEK укладено кут К;

б) ∆MNP укладено кут N?

Малюнок 2

Викликаю учня до дошки, він супроводжує свою відповідь демонстрацією на кресленнях та записом на дошці.

3. Вивчення нового матеріалу: ( 16 хв)

Щоб встановити рівність двох трикутників, треба їх поєднувати чи перевірити рівність відповідних сторін та відповідних кутів. Шість рівностей! Але іноді ні поєднати, ні перевірити усі шість рівностей немає можливості. Та це й не потрібно, виявляється достатньо встановити лише частину з них. Наша мета – визначити, які із шести цих рівностей справді необхідні.

Отже, маємо проблему.

Її рішенням і займемося.

Малюнок 3

Виявляється справедливе твердження «Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні». Це твердження називається "Перша ознака рівності трикутників".

А в математиці кожне твердження, справедливість якого встановлюється шляхом міркувань, називається теоремою, а самі міркування називаються доказом теореми.

Які теореми нам уже відомі?

Властивість суміжних кутів та властивість вертикальних кутів.

Чому ж теорема про рівність трикутників називається ознакою?

Ознака (за В.Далем) - це знак, відмінність, все, чому дізнаються що-небудь. Побачивши морозний візерунок на вікні, можна не виходячи з дому сказати, що на вулиці холодно. Щоб дізнатися, чи число 7859467 ділиться на 9, не обов'язково виконувати поділ: можна скористатися ознакою ділимості.

Ознака дає можливість встановлювати рівність двох трикутників, не проводячи фактичного накладання одного з них на інший, а порівнюючи лише деякі елементи трикутників.

Будь-яка теорема складається з умови та укладання. Як ви розумієте, що може означати словосполучення «умова теореми», а що – «укладання теореми»?

Умова – це вже відомі факти, про які йдеться у теоремі, а висновок – це те, що потрібно довести.

Виділіть умову теореми «Першої ознаки рівності трикутників».

Якщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам та куту між ними іншого трикутника.

Виділіть висновок теореми.

То такі трикутники рівні.

Отже, доведемо першу ознаку рівності трикутників:

А тепер розглянемо ще одне запитання. Але спочатку уважно послухайте формулювання: Якщо дві сторони і кут одного трикутника відповідно дорівнюють двом сторонам і куту іншого трикутника, то такі трикутники рівні. Як ви думаєте, чи правильне це твердження?

Розглянемо ∆ АВС та ∆АDС.

Малюнок 4

Сторона АВ трикутника АВС дорівнює стороні АD трикутника АDС, сторона АС – загальна, та С – загальний. Але трикутники не рівні. Отже, умова затвердження виконано, а висновок – ні. Значить твердження не так. Зверніть особливу увагу на те, що умова між ними необхідна!

4. Закріплення нового матеріалу: (10 хв)

Розглянемо, як можна застосувати теорему на вирішення завдань.

Усне вирішення завдань по готовим кресленням, заздалегідь заготовленим на звороті дошки чи слайді.

№2:

Для вирішення кожного завдання викликаю учня до дошки, де коментує рішення, показуючи згадані елементи на кресленні. Решта учнів слухає, поправляє, доповнює відповідь, якщо в цьому є необхідність.

Акцентую увагу учнів на обов'язковості змістовного посилання «трикутники рівні з двох сторін і куту між ними», а не формальної «трикутники рівні за першою ознакою», чи з'ясовую всім був зрозумілий хід рішення, якщо виникли питання, сама відповідаю на них.

Якщо в задачі знадобиться довести, що два трикутники рівні, чим слід скористатися: визначенням чи теоремою?

Звичайно, теорема. Відповідно до визначення потрібно трикутники поєднувати, а відповідно до теореми - перевірити три рівності.

На рис. АВ = АС, 1 = 2.

а) Доведіть, що трикутники АВD та АСD рівні;

б) знайдіть ВD та АВ, якщо АС=15 см, DC=5 см.

Дано: АВ = АС, 1 = 2,

АС=15 див, DC=5 див.

Довести:

∆АВD = ∆АСD.

Знайти: ВD, АВ.

Доведення: Перш ніж оформити рішення на дошці, пропоную учням усно вирішити завдання. Один учень коментуєДоведення. Інший – знаходження довжин відрізків. А потімзаписуємо розв'язання задачі: я на дошці, учні у зошиті.

Можливий запис рішення:

Доведення:

Розглянемо ∆АВD та ∆АСD.

АВ = АС (за умов.)

АD – загальна сторона ∆АВD = ∆АСD (по двох

1 = 2 (по ум.) сторонам і кутку між ними)

Словесний коментар: трикутники АВD і АСD рівні по двох сторонах і кут між ними, перша ознака рівності трикутників, в якому говориться: «Якщо дві сторони і кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні .»

ВD = DC = 5 см, АВ = АС = 15 см. (Як відповідні елементи рівних трикутників).

Відповідь: ВD = 5 см, АВ = 15см.

З'ясовую, чи не виникли питання щодо ходу рішення.

5. Підсумок уроку:(4 хв)

Отже, давайте повторимо:

Які трикутники називаються рівними?

Що називається теоремою?

Що називається доказом теореми?

Яку теорему ми сьогодні довели? Сформулюйте її.

Чому теорема називається ознакою?

Учні відповідають питання.

Виставляю оцінки за роботу на уроці із коментарем.

6. Домашнє завдання: ( 2 хв)

П 15. Запитання 3 -4 стор. 49-50. №93, 95.

№93. Відрізки АЕ і DC перетинаються в точці, що є серединою кожного з них. А) Доведіть, що трикутники АВС та ЕВD рівні; б) знайдіть кути А і С трикутника АВС, якщо у трикутнику ВDЕ D = 470, Е = 420.

№95. На рис. ВС=АD, 1 = 2, а) Доведіть, що трикутники АВС та СDА рівні; б)Знайдіть АВ і ВС, якщо АD = 17см, DС = 14см.

Список літератури:

Атанасян Л.С., Бутузов В.Ф. та ін. Геометрія 7-9 кл. Підручник для 7-9 класів середньої школи. - М: Просвітництво, 2006.

Атанасян Л.С., Бутузов В.Ф. та ін. Вивчення геометрії у 7-9 класах. Методичні поради до підручника. - М: Просвітництво, 2000.

Ковальова Г.І., Мазурова Н.І. Тести для поточного та узагальнюючого контролю. Видавництво "Вчитель" 2008. .

Амелькін В.В., Рабцевич Т.І. Шкільна геометрія у кресленнях та формулах. 2008.

Теорема 3.1 (ознака рівності трикутниківпо двох сторонах і кутку між ними).Якщо дві сторони і кутміж ними одного трикутника рівні відповідно до двох сторін і куту між ними іншого трикутника, такі трикутники рівні.

Доведення.Нехай у трикутників ABC і A1B1C1А=А1, AB=A1B1, АС=А1С1 (рис. 44). Доведемо, що трикутникирівні.

Нехай А 1 В 2 С 2 —трикутник, рівний трикутнику ABC, з вершиною В 2 на промені A 1 B 1 і вершиною С 2 у тій же напівплощині щодо прямої A 1 B 1 де лежить вершина C 1 (рис. 45, а ).

Так як A 1 B 1 = A 1 B 2 то вершина B 2 збігається з вершиною В 1 (рис. 45,6). Так як B 1 A 1 C 1 =B 2 A 1 C 2 то промінь А 1 С 2 збігається з променем A 1 C 1 (рис. 45, в). Оскільки A 1 C 1 =A 1 C 2 то вершина З 2 збігається з вершиною C 1 (рис. 45, г).

Отже, трикутник A 1 B 1 C 1 збігається з трикутником А 1 В 2 С 2 означає, що дорівнює трикутнику ABC. Теорему доведено.

Завдання (1). Відрізки АВ та CD перетинаються у точці О, яка є серединою кожного з них. Чому дорівнює відрізок BD, якщо відрізок АС = 10 м?

Рішення. Трикутники АОС та BOD рівні за першою ознакою рівності трикутників(Рис. 46).

Вони кути АОС і BOD рівні як вертикальні, а OA=ОВ і OC=OD оскільки точка О є серединою відрізків АВ і CD. З рівності трикутників АОС та BOD випливає рівність їх сторін АС та BD. Оскільки за умовою завдання АС = 10 м, то BD=10 м.

А. В. Погорєлов, Геометрія для 7-11 класів, Підручник для загальноосвітніх установ

Два трикутники називаються рівними, якщо їх можна поєднати накладенням. На малюнку 1 зображені рівні трикутники ABC і А1В1С1. Кожен із цих трикутників можна накласти на інший так, що вони повністю суміщаться, тобто попарно поєднаються їхні вершини та сторони. Ясно, що при цьому попарно поєднаються і кути цих трикутників.

Таким чином, якщо два трикутники рівні, то елементи (тобто сторони та кути) одного трикутника відповідно дорівнюють елементам іншого трикутника. Відмітимо, що у рівних трикутниках проти відповідно рівних сторін(тобто поєднуються при накладенні) лежать рівні кути,і назад: проти відповідно рівних кутів лежать рівні боки.

Так, наприклад, у рівних трикутниках ABC і A 1 B 1 C 1 , зображених на малюнку 1, проти відповідно рівних сторін АВ і А 1 В 1 лежать рівні кути З і С 1 . Рівність трикутників ABC і А1В1С1 позначатимемо так: ΔABC = ΔА1В1С1. Виявляється, що рівність двох трикутників можна встановити, порівнюючи деякі їх елементи.

Теорема 1. Перша ознака рівності трикутників.Якщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то такі трикутники рівні (рис.2).

Доведення. Розглянемо трикутники ABC і A 1 B 1 C 1 , які мають АВ = A 1 B 1 , АС = A 1 C 1 ∠ А = ∠ А 1 (див. рис.2). Доведемо, що ABC = A 1 B 1 C 1 .

Так як ∠ А = ∠ А 1 , то трикутник ABC можна накласти на трикутник А 1 В 1 С 1 так, що вершина А суміситься з вершиною А 1 , а сторони АВ та АС накладуться відповідно на промені А 1 В 1 та A 1 C 1 . Оскільки АВ = A 1 B 1 , АС = А 1 С 1 , то сторона АВ поєднається зі стороною А 1 В 1 а сторона АС - зі стороною А 1 C 1 ; зокрема, суміщаться точки і В 1 , З і C 1 . Отже, суміщаються сторони ЗС і В1С1. Отже, трикутники ABC і А 1 В 1 З 1 повністю суміщаються, отже, вони рівні.

Аналогічно шляхом накладання доводиться теорема 2.

Теорема 2. Друга ознака рівності трикутників.Якщо сторона і два кути одного трикутника, що прилягають до неї, відповідно рівні стороні і двом прилеглим до неї кутам іншого трикутника, то такі трикутники рівні (рис. 34).

Зауваження. На основі теореми 2 встановлюється теорема 3.

Теорема 3. Сума будь-яких двох внутрішніх кутів трикутника менша за 180°.

З останньої теореми випливає теорема 4.

Теорема 4. Зовнішній кут трикутника більший за будь-який внутрішній кут, не суміжний з ним.

Теорема 5. Третя ознака рівності трикутників.Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні ().

приклад 1.У трикутниках ABC та DEF (рис. 4)

∠ А = ∠ Е, АВ = 20 см, АС = 18 см, DE = 18 см, EF = 20 см. Порівняти трикутники ABC та DEF. Який кут у трикутнику DEF дорівнює куту?

Рішення. Дані трикутники дорівнюють за першою ознакою. Кут F трикутника DEF дорівнює куту трикутника ABC, так як ці кути лежать проти відповідно рівних сторін DE і АС.

приклад 2.Відрізки АВ та CD (рис. 5) перетинаються у точці О, яка є серединою кожного з них. Чому дорівнює відрізок BD, якщо відрізок АС дорівнює 6 м?

Рішення. Трикутники АОС та BOD рівні (за першою ознакою): ∠ АОС = ∠ BOD (вертикальні), АВ = ОВ, СО = OD (за умовою).
З рівності цих трикутників випливає рівність їх сторін, тобто АС = BD. Але оскільки за умовою АС = 6 м, то BD = 6 м.

Трикутник . Гострокутний, тупокутний та прямокутний трикутник.

Катети та гіпотенуза. Рівностегновий та рівносторонній трикутник.

Сума кутів трикутника.

Зовнішній кут трикутника. Ознаки рівності трикутників.

Чудові лінії та точки у трикутнику: висоти, медіани,

бісектриси,серединні e перпендикуляри, ортоцентр,

центр тяжкості, центр кола, центр вписаного кола.

Теорема Піфагора. Співвідношення сторін у довільному трикутнику.

Трикутник – це багатокутник із трьома сторонами (або трьома кутами). Сторони трикутника часто позначаються малими літерами, які відповідають великим літерам, що позначають протилежні вершини.

Якщо всі три кути гострі (рис.20), то це гострокутний трикутник . Якщо один із кутів прямий(C, рис.21), то це прямокутний трикутник; сторониa, b, що утворюють прямий кут, називаються катетами; сторонаc, протилежна прямому куту, називається гіпотенузою. Якщо один ізкутів тупий (B, рис.22), то це тупокутний трикутник.


Трикутник ABC (рис.23) - рівнобедрений, якщо двійого сторони рівні (a= c); ці рівні сторони називаються бічними, третя сторона називається основоютрикутник. Трикутник ABC (рис.24) - рівносторонній, якщо Усейого сторони рівні (a = b = c). У загальному випадку ( a ≠ b ≠ c) маємо нерівностороннійтрикутник .

Основні властивості трикутників. У будь-якому трикутнику:

1. Проти більшої сторони лежить більший кут, і навпаки.

2. Проти рівних сторін лежать рівні кути, і навпаки.

Зокрема, всі кути в рівностороннімтрикутнику рівні.

3. Сума кутів трикутника дорівнює 180 º .

З двох останніх властивостей випливає, що кожен кут у рівносторонньому

трикутнику дорівнює 60 º.

4. Продовжуючи одну із сторін трикутника (AC, рис.25), отримуємо зовнішній

кут BCD . Зовнішній кут трикутника дорівнює сумі внутрішніх кутів,

не суміжних з ним : BCD = A + B.

5. Будь-яка сторона трикутника менша від суми двох інших сторін і більше

їх різниці (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Ознаки рівності трикутників.

Трикутники рівні, якщо вони відповідно рівні:

a ) дві сторони та кут між ними;

b ) два кути і прилегла до них сторона;

c) три сторони.

Ознаки рівності прямокутних трикутників.

Два прямокутнихтрикутника рівні, якщо виконується одна з наступних умов:

1) рівні їх катети;

2) катет та гіпотенуза одного трикутника рівні катету та гіпотенузі іншого;

3) гіпотенуза та гострий кут одного трикутника рівні гіпотенузі та гострому куту іншого;

4) катет і прилеглий гострий кут одного трикутника дорівнюють катету та прилеглому гострому куту іншого;

5) катет і протилежний гострий кут одного трикутника дорівнюють катету і протилежному гострому кутку іншого.

Чудові лінії та точки у трикутнику.

Висота трикутника - цеперпендикуляр,опущений з будь-якої вершини на протилежний бік ( або її продовження). Ця сторона називаєтьсяосновою трикутника . Три висоти трикутника завжди перетинаютьсяв одній точцізваної ортоцентромтрикутник. Ортоцентр гострокутного трикутника (точка O , рис.26) розташований усередині трикутника, аортоцентр тупокутного трикутника (точка O , Мал.27) – зовні; Ортоцентр прямокутного трикутника збігається з вершиною прямого кута.

Медіана – це відрізок , що з'єднує будь-яку вершину трикутника із серединою протилежної сторони. Три медіани трикутника (AD, BE, CF, рис.28) перетинаються в одній точці O завжди лежить всередині трикутникаі є його центром важкості. Ця точка ділить кожну медіану щодо 2:1, рахуючи від вершини.

Бісектриса – це відрізок бісектрисикута від вершини до точки перетину з протилежною стороною. Три бісектриси трикутника (AD, BE, CF, рис.29) перетинаються в одній точці О, що завжди лежить усередині трикутникаі що є центром вписаного кола(Див. розділ «Вписаніта описані багатокутники»).

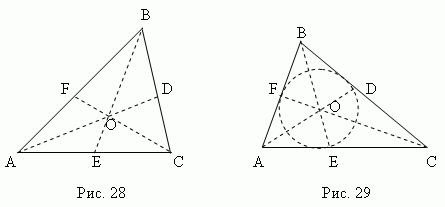
Бісектриса ділить протилежний бік на частини, пропорційні прилеглим сторонам ; наприклад, на рис.29 AE: CE = AB: BC.

Середній перпендикуляр – це перпендикуляр, проведений із середньоїточки відрізка (сторони). Три серединні перпендикуляри трикутника АВС(KO, MO, NO, рис.30 ) перетинаються в одній точці О, що є центром описаного кола (точки K, M, N – середини сторін трикутника ABC).

У гострокутному трикутнику ця точка лежить усередині трикутника; у тупокутному – зовні; у прямокутному - у середині гіпотенузи. Ортоцентр, центр тяжкості, центр описаного та центр вписаного кола збігаються лише у рівносторонньому трикутнику.

Теорема Піфагора. У прямокутному трикутнику квадрат довжинигіпотенузи дорівнює сумі квадратів довжин катетів.

Доказ теореми Піфагора очевидно випливає з рис.31. Розглянемо прямокутний трикутник ABC з катетами a, bта гіпотенузою c.

Збудуємо квадрат AKMB , використовуючи гіпотенузу AB як бік. Потімпродовжимо сторони прямокутного трикутника ABC так, щоб отримати квадрат CDEF сторона якого дорівнюєa + b.Тепер ясно, що площа квадрата CDEF дорівнює ( a + b) 2 . З іншого боку, ця площа дорівнює суміплощ чотирьох прямокутних трикутниківі квадрата AKMB, тобто

c 2 + 4 (ab / 2) = c 2 + 2 ab,

звідси,

c 2 + 2 ab= (a + b) 2 ,

і остаточно маємо:

c 2 =a 2 + b 2 .

Співвідношення сторін у довільному трикутнику.

У загальному випадку (для довільного трикутника) маємо:

c 2 =a 2 + b 2 – 2ab· cos C,

де C – кут між сторонамиaі b .