"Фотометрія ісз". Елементи орбіти

Закони Кеплера

Закони Кеплера - три емпіричні співвідношення, інтуїтивно підібрані Йоганном Кеплером на основі аналізу астрономічних спостережень Тихо Браге. Описують ідеалізовану геліоцентричну орбіту планети. У межах класичної механіки виводяться з розв'язання задачі двох тіл граничним переходом /→ 0, де, , - маси планети та Сонця відповідно.

Перший закон Кеплера (закон еліпсів):

Кожна планета Сонячна системазвертається за еліпсом, в одному з фокусів якого знаходиться Сонце. Форма еліпса і ступінь його подібності з колом характеризується ставленням, де відстань від центру еліпса до його фокусу (половина міжфокусної відстані), велика піввісь. Розмір називається ексцентриситетом еліпса. При, і, отже, еліпс перетворюється на коло.

Доказ першого закону Кеплера

Закон всесвітнього тяжіння Ньютона свідчить, що «кожен об'єкт у Всесвіті притягує кожен інший об'єкт по лінії, що з'єднує центри мас об'єктів, пропорційно масі кожного об'єкта, і обернено пропорційно квадрату відстані між об'єктами». Це передбачає, що прискорення має форму.

Згадаймо, що у полярних координатах:

У координатній формі запишемо:

Підставляючи і на друге рівняння, отримаємо

яке спрощується

Після інтегрування запишемо вираз

для деякої константи, яка є питомим кутовим моментом ().

Рівняння руху у напрямку стає рівним

Закон всесвітнього тяжіння Ньютона пов'язує силу на одиницю маси з відстанню як

де G – універсальна гравітаційна константа та M – маса зірки.

В результаті

Це диференціальне рівняння має загальне рішення:

для довільних констант інтегрування e та θ0.

Замінюючи u на 1/r і вважаючи θ0 = 0, отримаємо:

Ми отримали рівняння конічного перерізу з ексцентриситетом e та початком системи координат в одному з фокусів. Таким чином, перший закон Кеплера прямо випливає із закону всесвітнього тяжіння Ньютона та другого закону Ньютона.

Другий закон Кеплера (закон площ):

Кожна планета рухається в площині, що проходить через центр Сонця, причому за рівні проміжки часу радіус-вектор, що з'єднує Сонце та планету, визначає рівні площі.

Стосовно нашої Сонячної системи, із цим законом пов'язані два поняття: перигелій - найближча до Сонця точка орбіти, і афелій - найбільш віддалена точка орбіти. Таким чином, з другого закону Кеплера випливає, що планета рухається навколо Сонця нерівномірно, маючи велику перигелію лінійну швидкість, ніж у афелії.

Щороку на початку січня Земля, проходячи через перигелій, рухається швидше, тому видиме переміщення Сонця екліптикою на схід також відбувається швидше, ніж у середньому протягом року. На початку липня Земля, проходячи афелій, рухається повільніше, тому й переміщення Сонця екліптикою сповільнюється. Закон площ показує, що сила, яка керує орбітальним рухом планет, спрямована до Сонця.

Доказ другого закону Кеплера

За визначенням кутовий момент L точкової частки масою m і швидкістю v записується у вигляді:

де - радіус-вектор частки, а імпульс частинки. Площа, замітана радіус-вектором rза час dtз геометричних міркувань дорівнює

де є кут між напрямками rі v .

За визначенням

В результаті ми маємо

Продиференціюємо обидві частини рівняння за часом

оскільки векторний добуток паралельних векторів дорівнює нулю. Зауважимо, що F завжди паралельний r, оскільки радіальна сила, і p завжди паралельний v за визначенням. Отже можна стверджувати, що L , отже і пропорційна їй швидкість замітання площі - константа.

Третій закон Кеплера (гармонічний закон) ^

Квадрати періодів обігу планет навколо Сонця ставляться, як куби великих півосей орбіт планет. Справедливо не лише для планет, а й для їхніх супутників.

де T1 і T2 - періоди обігу двох планет навколо Сонця, а a1 і a2 - Довжини великих півосей їх орбіт.

Ньютон встановив, що гравітаційне тяжіння планети певної маси залежить лише від відстані до неї, а чи не від інших властивостей, як-от склад чи температура. Він також показав, що третій закон Кеплера не зовсім точний - насправді до нього входить і маса планети/

де M- маса Сонця, а m1 і m2 - Маси планет.

Оскільки рух і маса пов'язані, цю комбінацію гармонійного закону Кеплера і закону тяжіння Ньютона використовують визначення маси планет і супутників, якщо відомі їх орбіти і орбітальні періоди.

Параметри орбіти у площині:

У небесній механіці це траєкторія небесного тілау гравітаційному полі іншого тіла, що має значно більшу масу (планети, комети, астероїда в полі зірки). У прямокутній системі координат, початок якої збігається з центром мас, траєкторія може мати форму конічного перерізу (кола, еліпса, параболи або гіперболи). При цьому його фокус збігається із центром мас системи.

Кеплерові орбіти

Довгий час вважалося, що планети повинні мати кругову орбіту. Після довгих і безуспішних спроб підібрати кругову орбіту для Марса, Кеплер відкинув це твердження і, згодом, використовуючи дані вимірювань, зроблених Тихо Браге, сформулював три закони (див. Закони Кеплера), що описують орбітальний рух тел.

Кеплеровими елементами орбіти є:

фокальний параметр, велика піввісь, радіус перицентру, радіус апоцентру - визначають розмір орбіти,

ексцентриситет (е) - визначає форму орбіти,

спосіб орбіти (i),

довгота висхідного вузла () - визначає положення площини орбіти небесного тіла у просторі,

аргумент перицентру () - задає орієнтацію апарату в площині орбіти (часто задають напрямок на перицентр),

момент проходження небесного тіла через перицентр (To) – задає прив'язку за часом.

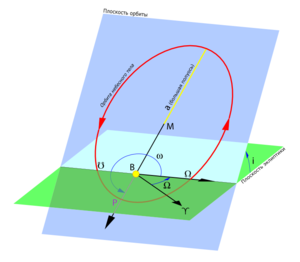
Ці елементи однозначно визначають орбіту незалежно від її форми (еліптичної, параболічної чи гіперболічної). Основний координатною площиноюможе бути площина екліптики, площина галактики, площина земного екватора і т. д. Тоді елементи орбіти задаються щодо обраної площини.

Елементи орбіти - шість величин, що визначають форму та розміри орбіти небесного тіла, її положення у просторі, а також положення самого небесного тіла на орбіті. Елементи орбіти описують закон руху небесного тіла: знаючи їх, можна визначити, у якій точці простору перебуває небесне тіло у будь-який заданий час.

Форма і розміри орбіти визначаються великою піввіссю орбіти () і ексцентриситетом орбіти:

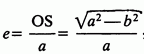
де b - мала піввісь орбіти. Для еліптичної орбіти значення ексцентриситету укладено не більше: . При e = 0 орбіта має форму кола; що ближче ексцентриситет до одиниці, то більше витягнута орбіта. При е=1 орбіта не замкнута і має вигляд параболи; при е>1 орбіта гіперболічна (див. Орбіти небесних тіл).

Орієнтація орбіти у просторі визначається щодо деякої площині, прийнятої за основну.

Для планет, комет та інших тіл Сонячної системи такою площиною є площина екліптики. Положення площини орбіти визначається двома елементами орбіти: довготою висхідного вузла Q і нахилом (нахилом) орбіти i. Довгота висхідного вузла - це кут при Сонці між лінією перетину площин орбіти та екліптики та напрямком на точку весняного рівнодення. Кут відраховується вздовж екліптики від точки весняного рівнодення у за годинниковою стрілкою до висхідного вузла орбіти Q, тобто тієї точки, в якій тіло перетинає екліптику, переходячи з південної півсфери в північну. (Протилежна точка називається низхідним вузлом, а лінія, що з'єднує вузли, - лінією вузлів.) Довгота висхідного вузла може мати значення від 0 до 360 °.

При вивченні руху штучних супутників Землі як основний беруть площину екватора; у цьому випадку лінія вузлів – це лінія перетину площин орбіти та небесного екватора. Її положення визначається прямим сходженням висхідного вузла, що відраховується від точки весняного рівнодення вздовж екватора (див. Небесна сфера).

Становище орбіти на площині Q визначається аргументом перигелію з, що є кутове відстань перигелія орбіти від висхідного вузла:. Аргумент перигелію відраховується у площині орбіти у бік руху небесного тіла і може мати будь-які значення від 0 до 360°. Для штучних супутників Землі цей елемент орбіти називається аргументом перигею.

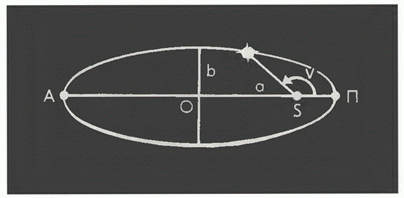
Як шостий елемент, що визначає положення небесного тіла на орбіті в якийсь певний момент часу, використовують момент проходження через перигелій. Положення тіла на орбіті у будь-який інший момент визначається за допомогою законів Кеплера. Кут при Сонці, відрахований від напрямку на перигелій до напрямку на тіло, називається істинною аномалією. Справжня аномалія під час руху тіла орбітою змінюється нерівномірно; відповідно до другого закону Кеплера тіло рухається швидше біля перигелія П і повільніше - у афелія А. Справжню аномалію обчислюють за відомими формулами за допомогою допоміжної величини, званої середньою аномалією М. Середня аномалія змінюється рівномірно, причому вона дорівнює 0 і 180° аномалією (тобто фіктивна точка, що визначає середню аномалію, проходить через перигелій та афелій у той же момент, що і реальне тіло).

Середню аномалію тіла в епоху (тобто в певний заданий момент часу, наприклад, на початку заданої доби) використовують часто замість шостого елемента. Іноді замість цього елемента задають - момент проходження тіла через висхідний вузол орбіти.

При відомої масі центрального тіла велика піввісь орбіти однозначно пов'язана із середнім рухом п тіла по орбіті і періодом звернення Р. Ці величини можуть задаватися в якості одного з елементів орбіти замість а.

Елементи орбіти постійні лише у випадку двох тіл (див. Небесна механіка). Якщо ж рух тіла впливає тяжіння третіх тіл чи будь-які інші сили (наприклад, опір атмосфери у разі штучних супутників Землі), то елементи орбіти безперервно повільно змінюються.

І тут поняття періоду звернення набуває кілька значень, залежно від цього, щодо якої точки він відраховується. Так, повний період звернення, відрахований щодо спрямування на ту чи іншу зірку, називається сидеричним періодом. Якщо період відраховується щодо перигелія, він носить назву аномалістичного періоду; якщо щодо висхідного вузла, то назва драконічного періоду. У разі незбуреного (кеплерівського) руху всі ці періоди мають однакове значення; при обуреному русі можуть істотно відрізнятися.