Дії з модулями чисел. Модуль числа (абсолютна величина числа), визначення, приклади, властивості

В математиці, як і в житті, часто зустрічаються ситуації, де негативні числа не мають ніякого практичного сенсу: наприклад, ми не можемо проїхати на машині кілометрів (ми проїдемо кілометрів, неважливо, в якому напрямку), як і не можемо купити кілограмів апельсинів. Ці значення завжди повинні бути позитивними. Саме тому в математиці існує спеціальний термін - модуль.

Що ж таке модуль числа?

Уяви, що це ти.

Припустимо, що ти стоїш на місці і можеш рухатися як вперед, так і назад. Позначимо точку відправлення.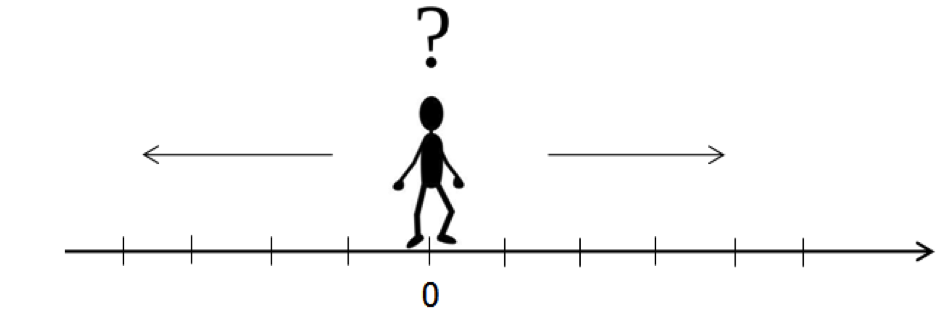



Отже, ти робиш крок вперед і опиняєшся в точці з координатою.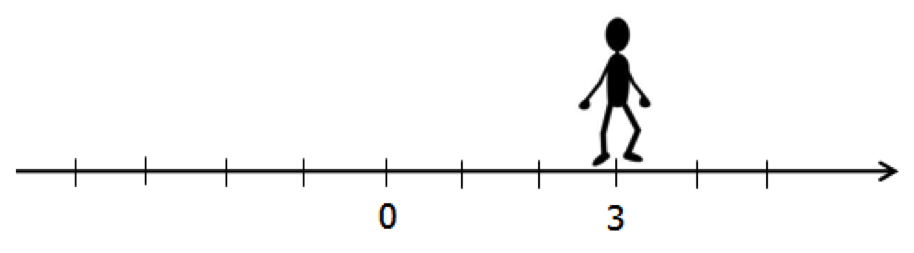



Це означає, що ти пішов від місця, де стояв на кроку(Одиничних відрізка). Тобто, відстаньвід початку руху до точки, де ти в підсумку виявився, так само.
Але ж ти ж можеш рухатися і назад!
Якщо від відправної точки з координатою зробити кроку в зворотну сторону, то опинишся в точці з координатою.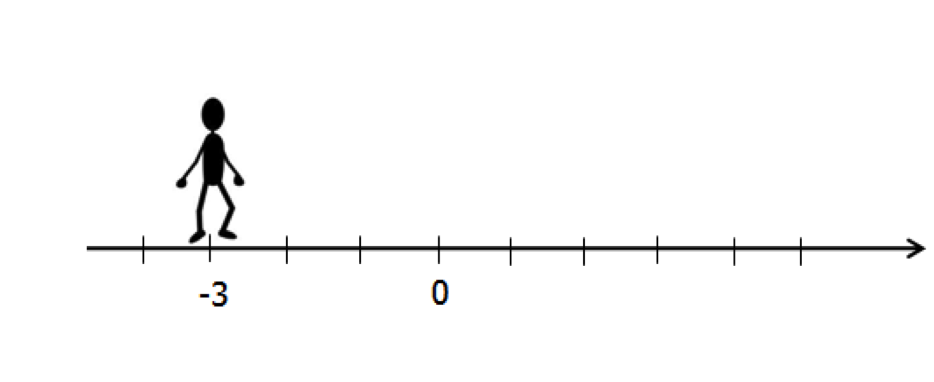



Яка відстань було пройдено в першому і в другому випадку? Звичайно ж, відстань, пройдену в першому і в другому випадку, буде однаковим і рівним трьом, адже обидві точки (і), в яких ти опинився однаково віддалені від точки, з якої було розпочато рух ().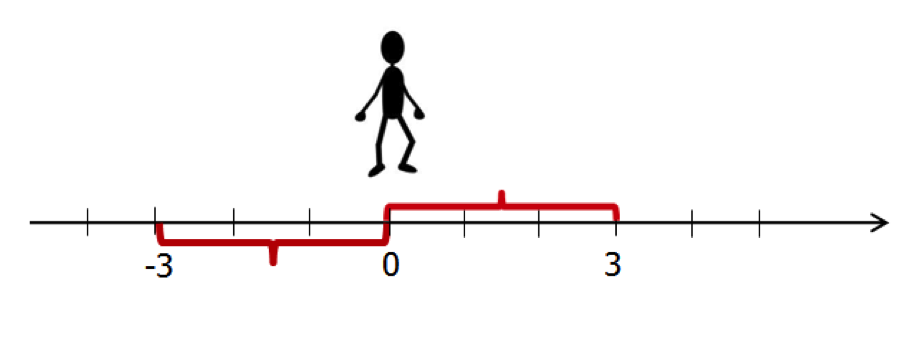



Таким чином, ми наблизилися до поняття модуля. Виходить, що модуль показує відстань від будь-якої точки на координатному відрізку до точки початку координат.
Так, модулем числа буде. Модуль числа також дорівнює, тому що відстань не може бути негативним!

Модуль - це абсолютна величина

Позначається модуль просто:

(- будь-яке число).

Отже, знайдемо модуль числа і:

Основні властивості модуля

Ось ми і наблизилися до першого властивості модуля: модуль не може бути виражений негативним числом.

Тобто, якщо - число позитивне, то його модуль буде дорівнює цьому ж числу.

якщо то.

Якщо - негативне число, то його модуль дорівнює протилежного числу:

якщо то

А якщо? Ну звичайно! Його модуль також дорівнює:

якщо, то, або.

З цього випливає, що модулі протилежних чисел рівні, тобто:

А тепер потренуйся:

Відповіді: 9; 3; 16; 8; 17.

Досить легко, правда?
А якщо перед тобою ось таке число:

Як бути тут? Як розкрити модуль в цьому випадку? Діємо за тим же сценарієм. Спочатку визначаємо знак вираження під знаком модуля, а потім розкриваємо модуль:

• якщо значення виразу більше нуля, то просто виносимо його з-під знака модуля,
• якщо ж вираз менше нуля, то виносимо його з-під знака модуля, змінюючи при цьому знак, як робили це раніше в прикладах.

Ну що, спробуємо? оцінимо:

(Забув, що таке корінь?)
Якщо, то який знак має? Ну звичайно, ! А, значить, знак модуля розкриваємо, змінюючи знак у вирази:

Розібрався? Тоді спробуй сам:

відповіді:

Якими ж ще властивостями володіє модуль?
По-перше, якщо нам потрібно перемножити числа всередині знака модуля, ми спокійно можемо перемножити модулі цих чисел. Тобто:

Висловлюючись математичною мовою, модуль твори чисел дорівнює добутку модулів цих чисел.

наприклад:

А що, якщо нам потрібно розділити два числа (вираження) під знаком модуля? Так то ж, що і з множенням! Розіб'ємо на два окремих числа (вираження) під знаком модуля:
за умови, що (так як на нуль ділити не можна).

Варто запам'ятати ще одну властивість модуля: модуль суми чисел завжди менше або дорівнює сумімодулів цих чисел:

Чому так? Все дуже просто! Як ми пам'ятаємо, модуль завжди позитивний. Але під знаком модуля може бути будь-яке число: як позитивне, так і негативне. Припустимо, що числа і обидва позитивні. Тоді ліве вираз дорівнюватиме правому висловом. Розглянемо на прикладі:

Якщо ж під знаком модуля одне число негативне, а інше позитивно, ліве вираз завжди виявиться менше правого:

Начебто з цим властивістю все ясно, розглянемо ще парочку корисних властивостеймодуля.
Що якщо перед нами такий вислів:

Що ми можемо зробити з цим виразом? Значення x нам невідомо, але зате ми вже знаємо, що, а значить. Число більше нуля, а значить можна просто записати:

Ось ми і прийшли до іншого властивості, яке в Загалом виглядіможна уявити так:

А чому дорівнює такий вислів:

Отже, нам необхідно визначити знак під модулем. А чи треба тут визначати знак? Звичайно, немає, якщо пам'ятаєш, що будь-яке число в квадраті завжди більше нуля! Якщо не пам'ятаєш, дивись тему. І що ж виходить? А ось що:

Здорово, так? Досить зручно. А тепер конкретний приклад для закріплення:

Ну, і чому сумніви? Діємо сміливо!

У всьому розібрався? Тоді вперед тренуватися на прикладах!

1. Знайдіть значення виразу, якщо.

2. У яких чисел модуль дорівнює?

3. Знайдіть значення виразів:

Якщо не всі поки ясно і є труднощі в рішеннях, то давай розбиратися:

рішення 1:

Отже, підставами значення і в вираз Отримаємо:

Рішення 2:

Як ми пам'ятаємо, протилежні числа по модулю рівні. Значить, значення модуля, рівне мають два числа: і.

Рішення 3:

а)
б)
в)
г)

Все вловив? Тоді пора перейти до складнішого!

Спробуємо спростити вираз

Рішення:

Отже, ми пам'ятаємо, що значення модуля не може бути менше нуля. Якщо під знаком модуля число позитивне, то ми просто можемо відкинути знак: модуль числа буде дорівнює цьому числу. Але якщо під знаком модуля негативне число, то значення модуля одно протилежного числу (тобто числу, взятому зі знаком «-»).
Для того, щоб знайти модуль будь-якого виразу, для початку потрібно з'ясувати, позитивне чи значення воно приймає, або негативне.

Виходить, значення першого виразу під модулем.

Отже, вираз під знаком модуля негативно. Другий вираз під знаком модуля завжди позитивно, так як ми складаємо два позитивних числа.

Отже, значення першого виразу під знаком модуля негативно, другого - позитивно: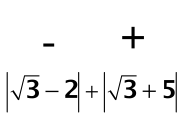

Це означає, розкриваючи знак модуля першого виразу, ми повинні взяти цей вислів зі знаком «-». Ось так:

У другому випадку просто відкинемо знак модуля.

У цій статті ми детально розберемо модуль числа. Ми дамо різні визначення модуля числа, введемо позначення і приведемо графічні ілюстрації. При цьому розглянемо різні приклади знаходження модуля числа за визначенням. Після цього ми перерахуємо і обгрунтуємо основні властивості модуля. В кінці статті поговоримо про те, як визначається і знаходиться модуль комплексного числа.

Навігація по сторінці.

Модуль числа - визначення, позначення і приклади

спочатку введемо позначення модуля числа. Модуль числа a будемо записувати як, тобто, ліворуч і праворуч від числа будемо ставити вертикальні рисочки, що утворюють знак модуля. Наведемо кілька прикладів. Наприклад, модуль -7 можна записати як; модуль 4,125 записується як, а модуль має запис виду.

Наступне визначення модуля відноситься до, а отже, і до, і до цілих, і до раціональних, і до ірраціональним числам, як до складників безлічі дійсних чисел. Про модулі комплексного числа ми поговоримо в.

Визначення.

Модуль числа a- це або саме число a, якщо a - позитивне число, або число -a, протилежне числу a, якщо a - негативне число, або 0, якщо a = 0.

Озвучене визначення модуля числа часто записують в наступному вигляді 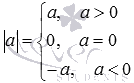, Цей запис означає, що, якщо a> 0,, якщо a = 0, і, якщо a<0 .

Запис можна уявити в більш компактній формі 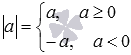. Цей запис означає, що, якщо (a більше або дорівнює 0), і, якщо a<0 .

Також має місце і запис 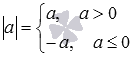. Тут окремо слід пояснити випадок, коли a = 0. У цьому випадку маємо, але -0 = 0, так як нуль вважають числом, яке протилежно самому собі.

Наведемо приклади знаходження модуля числаза допомогою озвученого визначення. Для прикладу знайдемо модулі чисел 15 і. Почнемо з знаходження. Так як число 15 - позитивне, то його модуль за визначенням дорівнює самому цьому числу, тобто,. А чому дорівнює модуль числа? Так як - негативне число, то його модуль дорівнює числу, протилежного числу, тобто, кількістю 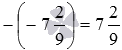. Таким чином, .

На закінчення цього пункту наведемо один висновок, який дуже зручно застосовувати на практиці при знаходженні модуля числа. З визначення модуля числа слід, що модуль числа дорівнює числу під знаком модуля без урахування його знака, А з розглянутих вище прикладів це дуже чітко видно. Озвучене твердження пояснює, чому модуль числа називають ще абсолютною величиною числа. Так модуль числа і абсолютна величина числа - це одне і те ж.

Модуль числа як відстань

Геометрично модуль числа можна інтерпретувати як відстань. Наведемо визначення модуля числа через відстань.

Визначення.

Модуль числа a- це відстань від початку відліку на координатної прямої до точки, що відповідає числу a.

Дане визначення узгоджується з визначенням модуля числа, даного в першому пункті. Пояснимо цей момент. Відстань від початку відліку до точки, якої відповідає позитивне число, так само цього числа. Нулю відповідає початок відліку, тому відстань від початку відліку до точки з координатою 0 дорівнює нулю (не потрібно відкладати жодного одиничного відрізка і жодного відрізка, що становить якусь частку одиничного відрізка, щоб від точки O потрапити в точку з координатою 0). Відстань від початку відліку до точки з негативною координатою дорівнює числу, протилежного координаті цієї точки, так як дорівнює відстані від початку координат до точки, координатою якої є протилежне число.

Наприклад, модуль числа 9 дорівнює 9, так як відстань від початку відліку до точки з координатою 9 дорівнює дев'яти. Наведемо ще приклад. Точка з координатою -3,25 знаходиться від точки O на відстані 3,25, тому .

Озвучене визначення модуля числа є окремим випадком визначення модуля різниці двох чисел.

Визначення.

Модуль різниці двох чисел a і b дорівнює відстані між точками координатної прямої з координатами a і b.

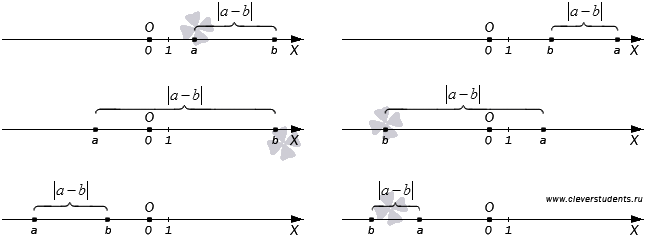
Тобто, якщо дано точки на координатній прямій A (a) і B (b), то відстань від точки A до точки B одно модулю різниці чисел a і b. Якщо в якості точки В взяти точку O (початок відліку), то ми отримаємо визначення модуля числа, наведене на початку цього пункту.

Визначення модуля числа через арифметичний квадратний корінь

іноді зустрічається визначення модуля через арифметичний квадратний корінь.

Для прикладу обчислимо модулі чисел -30 і на підставі даного визначення. Маємо. Аналогічно обчислюємо модуль двох третин: .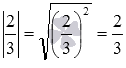

Визначення модуля числа через арифметичний квадратний корінь також узгоджується з визначенням, даним в першому пункті цієї статті. Покажемо це. Нехай a - позитивне число, при цьому число -a - негативне. тоді і , Якщо ж a = 0, то .

властивості модуля

Модулю притаманний ряд характерних результатів - властивості модуля. Зараз ми наведемо основні і найбільш часто використовувані з них. При обгрунтуванні цих властивостей ми будемо спиратися на визначення модуля числа через відстань.

Почнемо з самого очевидного властивості модуля - модуль числа не може бути негативним числом. У буквеному вигляді це властивість має запис виду для будь-якого числа a. Це властивість дуже легко обґрунтувати: модуль числа є відстань, а відстань не може виражатися негативним числом.

Переходимо до наступного властивості модуля. Модуль числа дорівнює нулю тоді і тільки тоді, коли це число є нуль. Модуль нуля є нуль за визначенням. Нулю відповідає початок відліку, ніяка інша точка на координатній прямій нулю не відповідає, так як кожному дійсному числу поставлено у відповідність єдина точка на координатній прямій. З цієї ж причини будь-якого числа, відмінного від нуля, відповідає точка, відмінна від початку відліку. А відстань від початку відліку до будь-якої точки, відмінною від точки O, не дорівнює нулю, так як відстань між двома точками дорівнює нулю тоді і тільки тоді, коли ці точки співпадають. Наведені міркування доводять, що нулю дорівнює лише модуль нуля.

Йдемо далі. Протилежні числа мають рівні модулі, тобто, для будь-якого числа a. Дійсно, дві точки на координатній прямій, координатами яких є протилежні числа, знаходяться на однаковій відстані від початку відліку, значить модулі протилежних чисел рівні.

Наступне властивість модуля таке: модуль твори двох чисел дорівнює добутку модулів цих чисел, тобто, . За визначенням модуль твори чисел a і b дорівнює або a · b, якщо, або - (a · b), якщо. З правил множення дійсних чисел слід, що твір модулів чисел a і b дорівнює або a · b,, або - (a · b), якщо, що доводить аналізованих властивість.

Модуль частки від розподілу a на b дорівнює частці від ділення модуля числа a на модуль числа b, тобто, . Обґрунтуємо це властивість модуля. Так як приватна дорівнює добутку, то. В силу попереднього властивості маємо 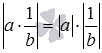. Залишилося лише скористатися рівністю, яке справедливо в силу визначення модуля числа.

Наступне властивість модуля записується у вигляді нерівності: , A, b і c - довільні дійсні числа. Записане нерівність є ні що інше як нерівність трикутника. Щоб це стало зрозуміло, візьмемо точки A (a), B (b), C (c) на координатній прямій, і розглянемо вироджених трикутник АВС, у якого вершини лежать на одній прямій. За визначенням модуля різниці дорівнює довжині відрізка АВ, - довжині відрізка АС, а - довжині відрізка СВ. Так як довжина будь-якого боку трикутника не перевищує суму довжин двох інших сторін, то справедливо нерівність , Отже, справедливо і нерівність.

Тільки що доведене нерівність набагато частіше зустрічається у вигляді . Записане нерівність зазвичай розглядають як окреме властивість модуля з формулюванням: « Модуль суми двох чисел не перевищує суму модулів цих чисел». Але нерівність безпосередньо випливає з нерівності, якщо в ньому замість b покласти -b, і прийняти c = 0.

Модуль комплексного числа

дамо визначення модуля комплексного числа. Нехай нам дано комплексне число, Записане в алгебраїчній формі, де x і y - деякі дійсні числа, що представляють собою відповідно дійсну і уявну частини даного комплексного числа z, а - уявна одиниця.

Модуль числа n являє собою кількість одиничних відрізків від початку координат до точки n. Причому не важливо, в який бік буде відраховуватися яку - вправо або вліво від нуля.

Спонсор розміщення P & G Статті по темі "Як знайти модуль числа" Як витягти з модуля Як обчислити модуль числа Як звести комплексне число в ступінь

Інструкція

Модуль числа також прийнято називати абсолютною величиною цього числа. Він позначається короткими вертикальними лініями, проведеними зліва і праворуч від числа. Наприклад, модуль числа 15 записується в такий спосіб: | 15 |.

Пам'ятайте, що модуль може бути тільки позитивним числом або нулем. Модуль позитивного числа дорівнює самому числу. Модуль нуля дорівнює нулю. Тобто для будь-якого числа n, яке більше або дорівнює нулю, буде справедлива наступна формула | n | = N. Наприклад, | 15 | = 15, тобто модуль числа 15 дорівнює 15-ти.

Модулем від'ємного числа буде те саме число, але з протилежним знаком. Тобто для будь-якого числа n, яке менше нуля, буде справедлива формула | n | = -N. Наприклад, | -28 | = 28. Модуль числа -28 дорівнює 28-ми.

Можна знаходити модулі не тільки для цілих, але і для дрібних чисел. Причому щодо дрібних чисел діють ті ж правила. Наприклад, | 0,25 | = 25, тобто модуль числа 0,25 дорівнюватиме 0,25. А | -? | =?, Тобто модуль числа -? буде дорівнює ?.

При роботі з модулями корисно знати, що модулі протилежних чисел завжди дорівнюють один одному, тобто | n | = | -N |. Це є основною властивістю модулів. Наприклад, | 10 | = | -10 |. Модуль числа 10 дорівнює 10-ти, точно так же, як модуль числа -10. Крім того, | a - b | = | B - a |, так як відстань від точки a до точки b і відстань від b до a дорівнюють один одному. Наприклад, | 25 - 5 | = | 5 - 25 |, тобто | 20 | = | - 20 |.

як просто

Інші новини по темі:

Слово «модуль» походить від латинського modulus, яке, в свою чергу, є зменшувально формою слова modus - міра. Таким чином, modulus приблизно перекладається як «маленька міра», «деталь». Спонсор розміщення P & G Статті по темі "Що таке модуль" Як помножити вектор на число Як

Комплексним числом називають число виду z = x + i * y, де x і y - дійсні числа, а i = уявна одиниця (тобто число, квадрат якого дорівнює -1). Щоб визначити поняття аргументу комплексного числа, необхідно розглянути комплексне число на комплексній площині в полярній системі координат.

Модулем числа x або її абсолютною величиною називається конструкція виду | x |. В узагальненому сенсі модуль - це норма елемента багатовимірного векторного простору і позначається як || x ||. Модуль числа не може бути негативним, для одного і того ж числа взятого з протилежними знаками,

Арифметичні дії з негативними числами людині доводиться виконувати досить часто. Найпоширеніший випадок пов'язаний з вимірами вуличної температури. Наприклад, вам потрібно дізнатися, на скільки градусів температура піднялася або опустилася в порівнянні з попереднім днем. Зі складанням та

З курсу шкільної математики багато хто пам'ятає, що корінь - це рішення рівняння, тобто ті значення Х, при яких досягається рівність його частин. Як правило, завдання знаходження модуля різниці коренів ставиться щодо квадратних рівнянь, адже саме вони можуть мати два кореня, різниця

Комплексними називаються числа виду z = a + bi, де a - дійсна частина, що позначається Re z, b - уявна частина, що позначається Im z, i - уявна одиниця. Безліч комплексних чисел є розширення множини дійсних чисел і позначається символом C. Над комплексними числами можна

Абсолютне значення числа - модуль - показує, наскільки відрізняється це число від нуля. Брати по модулю можна будь-які величини - від нескінченності в негативній частині шкали, до нескінченності в позитивній, але результат цієї операції завжди буде позитивний, якщо початкове значення відрізняється від